Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Контрольная работа № 4 по теме Степень с натуральным показателем - ОДНОЧЛЕНЫ - СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
Ход урока
I. Сообщение темы и цели урока
II. Общая характеристика контрольной работы
Контрольная работа составлена в шести вариантах (варианты 1,2 — самые простые, варианты 3, 4 — средней сложности, варианты 5, 6 — самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка “3” ставится за любые три решенные задачи, оценка “4” — за четыре задачи и оценка “5” — за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5,6 — дополнительно 1 балл (т. е. оценка “5” выставляется уже за четыре задачи). Все задачи в варианте примерно равноценны. Возможно, несколько труднее для учеников задачи 5, 6.
Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов.
Контрольная работа рассчитана на один урок.
III. Контрольная работа
Вариант 1
1. Дана функция у = х2 + 2. Составьте таблицу значений функции в промежутке -2 ≤ х ≤ 2 с шагом 0,5 и постройте график функции.
2. Выполните действия:
![]()
3. Запишите в виде одночлена стандартного вида выражение:
![]()
4. Сравните числа 816 и 216 ∙ 415.
5. Решите уравнение:
![]()
6. Докажите, что число 1050 - 4 делится на 3.
Вариант 2
1. Дана функция у = 1 - х2. Составьте таблицу значений функции в промежутке -2 ≤ х ≤ 2 с шагом 0,5 и постройте график функции.
2. Выполните действия:
![]()
3. Запишите в виде одночлена стандартного вида выражение:
![]()
4. Сравните числа 1014 и 215 ∙ 514.
5. Решите уравнение:
![]()
6. Докажите, что число 1040 - 7 делится на 3.
Вариант 3
1. Дана функция у = х2 - 2х. Составьте таблицу значений функции в промежутке -1 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Выполните действия:

3. Запишите в виде одночлена стандартного вида выражение:
![]()
4. Сравните числа 230 и 320.
5. Решите уравнение:
![]()
6. Докажите, что число 196374 + 391164 - 2 делится на 5.
Вариант 4
1. Дана функция у = х2 + 2х. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 1 с шагом 0,5 и постройте график функции.
2. Выполните действия:

3. Запишите в виде одночлена стандартного вида выражение:
![]()
4. Сравните числа 340 и 430.
5. Решите уравнение:
![]()
6. Докажите, что число 171536 + 375164 + 4 делится на 5.
Вариант 5
1. Дана функция у = х2 + 2|х|. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Запишите в виде одночлена стандартного вида выражение:
![]()
3. Сравните числа 780 и 4120.
4. Определите последнюю цифру числа (389)162 + (635)236.
5. Решите уравнение ![]()
6. Докажите, что число 10316 + 6 не делится на число 1019 - 1.
Вариант 6
1. Дана функция у = 2|х| - х2. Составьте таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5 и постройте график функции.
2. Запишите в виде одночлена стандартного вида выражение:
![]()
3. Сравните числа 960 и 490.
4. Определите последнюю цифру числа (289)364 + (536)171.
5. Решите уравнение ![]()
6. Докажите, что число 10273 + 7 не делится на число 1019 - 1.
IV. Подведение итогов контрольной работы
1. Распределение работ по вариантам и результаты решения. Данные удобно заносить в таблицу (для каждой пары вариантов).
|
№ задачи |
Итоги |
|||
|
+ |
± |
- |
Ø |
|
|
1 |
5 |
1 |
1 |
1 |
|
2 |
||||
|
... |
||||
|
6 |
||||
Обозначения:
+ — число решивших задачу правильно или почти правильно;
± — число решивших задачу со значительными погрешностями;
- — число не решивших задачу;
Ø — число не решавших задачу.
Варианты 1, 2 — 8 учащихся.
2. Типичные ошибки при решении задач.
3. Задачи, вызвавшие наибольшие трудности.
V. Разбор задач (ответы и решения)
Вариант 1

6. Доказано.
Вариант 2
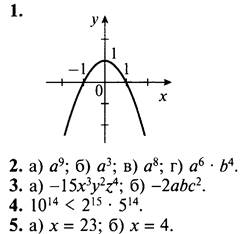
6. Доказано.
Вариант 3
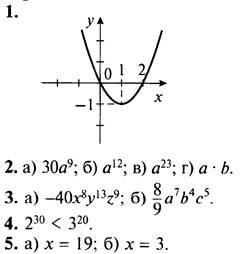
6. Доказано.
Вариант 4
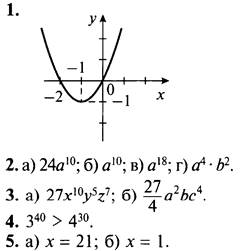
6. Доказано.
Вариант 5
1. Для функции у = х2 - 2|х| составим таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5.
|
x |
-3 |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y |
3 |
1,25 |
0 |
-0,75 |
-1 |
-0,75 |
0 |
-0,75 |
-1 |
-0,75 |
0 |
1,25 |
3 |
Отметим точки из таблицы на координатной плоскости и построим график данной функции. Легко проверить, что функция является четной и ее график симметричен относительно оси ординат.
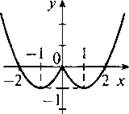
2. Используя правила действий со степенями, запишем одночлен в стандартном виде:
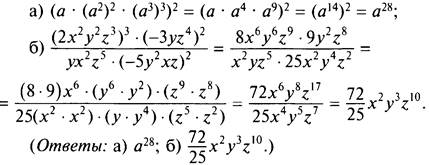
3. Запишем данные числа 780 и 4120 в другом виде: 780 = (72)40 = 4940 и 4120 = (43)40 = 6440. Так как 49 < 64, тo и 4940 < 6440, или 780 < 4120.
(Ответ: 780 < 4120.)
4. Запишем данное число в следующем виде: (389)162 + (635)236 = (3892)81 + (635)236. Число 389 оканчивается цифрой 9. При возведении в квадрат число 3892 оканчивается цифрой 1. Если число оканчивается цифрой 1 или 5, то при возведении такого числа в любую степень оно также будет оканчиваться цифрой 1 или 5. Поэтому данное число оканчивается цифрой 1 + 5 = 6.
(Ответ: 6.)
5. Используя свойства степеней, преобразуем данное уравнение:
![]() Найдем сумму чисел
Найдем сумму чисел ![]()
![]() Тогда уравнение имеет вид
Тогда уравнение имеет вид ![]()
Так как равны степени с одинаковым основанием 2, то равны и показатели степеней: 3х + 5 = 50 или 3x = 45, откуда x = 15.
(Ответ: х = 15.)
6. Рассмотрим число 10316 + 6. Число 10316 состоит из одной единицы и 316 нулей. Тогда число 10316 + 6 имеет вид 100...06. Сумма цифр этого числа равна 7, и по признаку делимости оно не делится на 9. Число 1019 состоит из одной единицы и 19 нулей. Поэтому число 1019 - 1 состоит из 19 девяток (т. е. 99...9) и делится на 9. Так как первое число 10316 + 6 не имеет делителя 9, то оно не может без остатка делиться на второе число 1019 - 1.
(Ответ: доказано.)
Вариант 6
1. Для функции 2|х| - х2 составим таблицу значений функции в промежутке -3 ≤ х ≤ 3 с шагом 0,5.
|
x |
-3 |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y |
-3 |
1,25 |
0 |
0,75 |
1 |
0,75 |
0 |
0,75 |
1 |
0,75 |
0 |
-1,25 |
-3 |
Отметим эти точки на координатной плоскости и построим график данной функции. Эта функция является четной, и ее график симметричен относительно оси ординат.
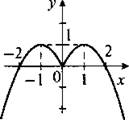
2. Используя правила действий со степенями, запишем одночлен в стандартном виде:
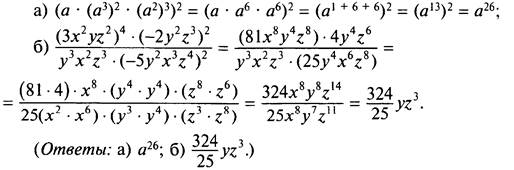
3. Запишем данные числа 960 и 490 в другом виде: 960 = (92)30 = 8130 и 490 = (43)30 = 6430. Так как 81 > 64, то и 8130 > 6430, или 960 > 490.
(Ответ: 960 > 490.)
4. Запишем данное число в следующем виде: (289)364 + (536)171 = (2892)182 + (536)171. Число 289 оканчивается цифрой 9. При возведении в квадрат число 2892 оканчивается цифрой 1. При возведении такого числа в любую степень оно будет также оканчиваться цифрой 1. Число 536 оканчивается цифрой 6. При возведении такого числа в любую степень оно будет также оканчиваться цифрой 6. Поэтому данное число оканчивается цифрой 1 + 6 = 7.
(Ответ: 7.)
5. Используя свойства степеней, преобразуем данное уравнение:
![]()
Найдем сумму чисел: ![]()
![]() Тогда уравнение имеет вид
Тогда уравнение имеет вид ![]()
Так как равны степени чисел с одинаковым основанием 3, то равны и показатели степеней: 4x + 4 = 68 или 4x = 64, откуда х = 16.
(Ответ: х = 16.)
6. Рассмотрим число 10273 + 7. Число 10273 состоит из одной единицы и 273 нулей. Тогда число 10273 + 7 состоит из одной единицы, 273 нулей и цифры 7, т. е. имеет вид 100...07. Сумма цифр этого числа равна 8, и по признаку делимости оно не делится на 9. Число 1019 состоит из одной единицы и 19 нулей. Поэтому число 1019 - 1 состоит из 19 девяток (т. е. 99...9). Очевидно, что такое число делится на 9, так как каждая цифра числа делится на 9. Следовательно, число 10273 + 7 не делится на число 1019 - 1 без остатка, так как не имеет делителя 9.
(Ответ: доказано.)
VI. Подведение итогов урока