Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. ТЕОРЕМА О ВНЕШНЕМ УГЛЕ ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цели деятельности учителя |
Создать условия для закрепления знаний учащихся о сумме углов треугольника при решении задач, введения понятия внешнего угла треугольника, доказательства теоремы о внешнем угле треугольника, обучения решению задач |
|||
|
Термины и понятия |
Треугольник, внешний угол, смежный угол |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий, умеют формулировать и доказывать теорему о внешнем угле треугольника |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Чертежи к задачам. • Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень сформированности теоретических знаний |
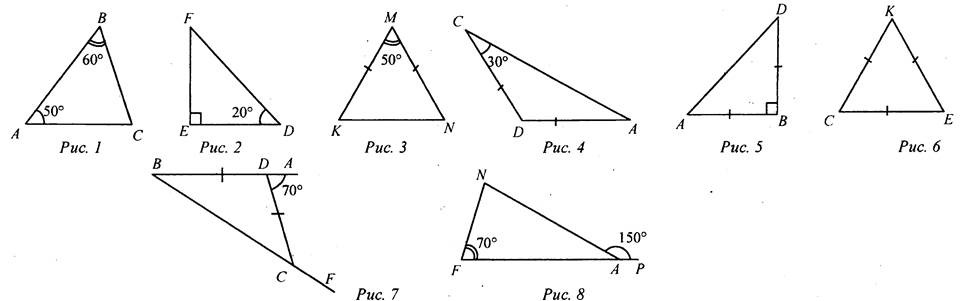
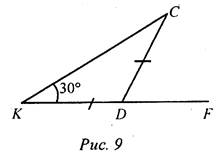
(Ф/И) 1. Один учащийся на доске доказывает теорему о сумме углов треугольника. 2. Второй учащийся решает на доске задачу из домашнего задания № 230. 3. Весь класс решает задачи по готовым чертежам (устно). Вычислите все неизвестные углы треугольников.
|
|||
|
II этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие внешнего угла и доказать сопутствующую теорему |
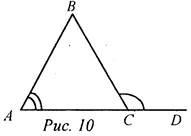
(Ф/И) 1. Ввести понятие внешнего угла треугольника. 2. Доказать теорему о внешнем угле треугольника (рис. 125 учебника). 3. Решить задачу (устно). В треугольнике ABC ∠В = 110°. Чему равны: а) сумма остальных внутренних углов треугольника; б) внешний угол при вершине В? 4. По готовому чертежу на доске устно решить задачу. Найдите внутренние углы и внешний угол CDF треугольника KCD
|
|||
|
III этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
При решении простейших задач отработать изученный материал |
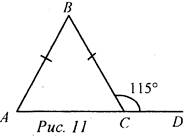
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 232 под руководством учителя на доске и в тетрадях. 2. Рассмотреть обратное утверждение: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании. Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника. 3. Решить задачу № 234 на доске и в тетрадях (рассмотреть два случая) |
№ 232. Дано: ΔABC, ∠BCD > ∠A в 2 раза. Доказать: ΔАВС - равнобедренный.
Доказательство: Примем ∠A = х, тогда ∠BCD = 2х. По свойству внешнего угла: ∠BCD = ∠A + ∠B, тогда 2х = х + ∠B, тогда ∠B = х, значит, ∠A = ∠B, то есть ΔАВС — равнобедренный. Обратное утверждение верно. № 234. Дано: ΔАВС, АВ = ВС, ∠BCD = 115°. Найти: ∠A, ∠B, ∠C.
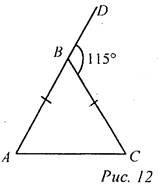
Решение: 1) ∠C, ∠BCD - смежные, значит, ∠C = 180° - 115° = 65°. 2) ∠A = ∠C = 65° (по свойству равнобедренного треугольника). 3) ∠B = 180° - (∠A + ∠C). ∠B = 180° - 130° = 50°. Ответ: 65°, 65°, 50°. Дано: ΔАВС, АВ = ВС, ∠CBD = 115°. Найти: ∠A, ∠B, ∠C.
Решение: 1) ∠B, ∠CBD - смежные, значит, ∠B = 180° - 115° = 65°. 2) Так как ∠A = ∠C (по свойству равнобедренного треугольника), то ∠A = ∠C = (180° - 65°): 2 = 57,5° = 57°30'. Ответ: 65°, 57°30', 57°30' |
||
|
IV этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Совершенствовать навыки самостоятельного решения задач |
(И) Работа выполняется 15-20 минут. Вариант I 1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника. 2. В треугольнике CDE с углом ∠E = 32° проведена биссектриса CF, ∠CFD = 72°. Найдите ∠D. Вариант II 1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника. 2. В треугольнике CDE проведена биссектриса CF, ∠D = 68°, ∠E = 32°. Найдите ∠CFD. Вариант III 1. В равнобедренном треугольнике MNP с основанием МР и углом ∠N = 64° проведена высота МН. Найдите ∠PMH. 2. В треугольнике CDE проведены биссектрисы СК и DP, пересекающиеся в точке F, причем ∠DFK = 78°. Найдите ∠CED. Вариант IV 1. В равнобедренном треугольнике CDE с основанием СЕ и ∠D = 102° проведена высота СН. Найдите ∠DCH. 2. В треугольнике ABС проведены биссектрисы AM и BN, пересекающиеся в точке К, причем ∠AKN = 58°. Найдите ∠ACB. |
|||
|
V этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Какой угол называется внешним углом треугольника? - Каким свойством обладает внешний угол равнобедренного треугольника? - Оцените свою работу на уроке. Поставьте себе оценку. Какие затруднения у вас возникли? |
||||