ТЕОРЕМА О СООТНОШЕНИЯХ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цель деятельности учителя

Создать условия для рассмотрения теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; для обучения применению этих знаний при решении задач

Термины и понятия

Треугольник, противолежащий угол, сторона

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев.

Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения.

Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Чертежи к задачам

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Провести анализ ошибок, допущенных в самостоятельной работе

(Ф/И)

1. Анализ результатов самостоятельной работы.

2. Обсуждение вопросов учащихся по домашнему заданию

II этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Рассмотреть теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем

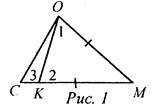
(Ф/И) о

1. Решить подготовительную задачу.

Дано: ΔМОС; К ∈ МС; КМ = ОМ.

Доказать: 1) ∠1 > ∠3; 2) ∠MOC > ∠3.

Доказательство:

1) Треугольник ОМК - равнобедренный с основанием ОК, поэтому ∠1 = ∠2. Угол 2 - внешний угол треугольника ОКС, поэтому ∠2 > ∠3. Значит, ∠1 = ∠2 и ∠2 > ∠3, следовательно, ∠1 > ∠3.

2) Так как точка К лежит на МС, то ∠MOC > ∠1, а так как ∠1 > ∠3, то ∠MOC > ∠3.

2. Сформулировать и доказать первое утверждение теоремы: в треугольнике против большей стороны лежит больший угол (по рис. 127 учебника).

3. Решить задачу № 236 (устно).

4. Перед доказательством второго утверждения теоремы (в треугольнике против большего угла лежит большая сторона) напомнить учащимся, какая теорема называется обратной данной, и предложить привести примеры обратных теорем, изученных ранее.

5. Сформулировать утверждение, обратное первому утверждению (самостоятельно).

6. Доказать обратное утверждение (методом от противного).

После того как сформулирована обратная теорема, записаны ее условие и заключение, полезно вспомнить, что при сравнении двух отрезков, например CD и EF, возможен один и только один из трех случаев: CD > EF; CD = EF; CD < EF. Поэтому если мы предполагаем, что CD не больше EF, то возможны два случая: либо CD = EF, либо CD < EF. После этих предварительных рассуждений учащимся легче понять, почему при доказательстве теоремы, предположив, что АВ не больше АС, мы рассматриваем два возможных случая: либо АВ = АС, либо АВ < АС.

7. Решить задачу № 237 (устно).

8. Доказать следствие 1 (самостоятельно).

9. Доказать следствие 2, выражающее признак равнобедренного треугольника (с помощью учителя)

III этап. Решение задач

Цель деятельности

Совместная деятельность

Научить применять полученные теоретические знания при решении задач

(Ф/И)

1. Решить задачи по готовым чертежам.

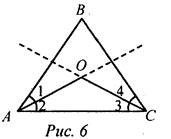
1) Дано: ∠А = ∠В (рис. 2).

Доказать: ΔАВС - равнобедренный.

2) Сравните углы ΔАВС (рис. 3).

3) Укажите наибольшую и наименьшую стороны ΔАВС (рис. 4).

4) Сравните отрезки AD и DC (рис. 5).

2. Решить задачу № 240 на доске и в тетради. В № 240.

Дано: ΔАВС, АВ = ВС, АО - биссектриса ∠A, СО - биссектриса ∠C.

Доказать: ΔАОС - равнобедренный.

Доказательство:

1) Так как ΔАВС - равнобедренный, то ∠A = ∠C.

2) Так как АО, СО - биссектрисы соответственно равных углов, то ∠1 = ∠2 = ∠3 = ∠4.

3) Рассмотрим ΔАОС: ∠2 = ∠3, тогда АО = СО, значит, ΔАОС - равнобедренный по определению

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие теоремы изучены на уроке?

- Оцените свою работу на уроке.

- Задайте три вопроса по теме урока

(И) Домашнее задание: изучить п. 33; ответить на вопросы 6-8 на с. 88; решить задачи № 239, 241