Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ. РЕШЕНИЕ ЗАДАЧ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для закрепления основных свойств прямоугольных треугольников, рассмотрения признака прямоугольного треугольника и свойства медианы прямоугольного треугольника; совершенствовать навыки решения задач на применение свойств прямоугольного треугольника |
||||
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для | решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||||
|
Образовательные ресурсы |
• Задания для фронтальной работы |
||||
|
I этап. Актуализация опорных знаний учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Проверить теоретическую подготовленность учащихся |
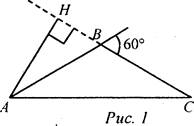
(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Заполнить пропуски в решении задач. 1) В равнобедренном треугольнике один из внешних углов равен 60°, высота, проведенная к боковой стороне, равна 5 см. Найдите основание треугольника.
Решение: Так как внешний угол равен 60°, то смежный с ним внутренний угол равен ... Этот угол может быть только углом, противолежащим основанию, так как он ... Так как ΔАВС - равнобедренный е основанием АС, то ∠A = ... = ... Так как АН - высота, то ΔАНС - ... В ΔАНС ∠C = 30°, значит, АН = ... Так как АН = 5 см, то АС = ... Ответ: АС =... 2) Высота и медиана, проведенные из одной вершины треугольника, разделили его угол на три равные части. Найдите углы треугольника.
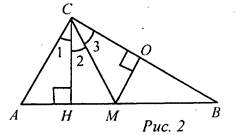
Решение: Пусть СН - высота, СМ - медиана ΔABC, ∠1 = ∠2 = ∠3. Проведем ОМ ⊥ СВ, тогда ΔАСН = ΔМСН по ... ΔСМН = ΔСМО по ... Тогда АН = НМ = МО = 1/2МА = 1/2МВ. Ответ: ∠Z = 60°, ∠B = 30°, ∠C = 90°. После обсуждения нужно отметить, что эти две задачи характеризуют дополнительные свойства прямоугольных треугольников: 1) Свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла: В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы. 2) Признак прямоугольного треугольника: Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный |
||||
|
II этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Совершенствовать навыки решения задач |
(Ф/И) Организует деятельность учащихся. 1. Решение задачи с подробным обсуждением: Гипотенуза прямоугольного треугольника в четыре раза больше проведенной к ней высоты. Найдите острые углы треугольника. (Г) 2. Самостоятельное решение задач с последующей самопроверкой по готовым ответам.
|
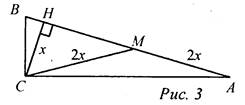
1.
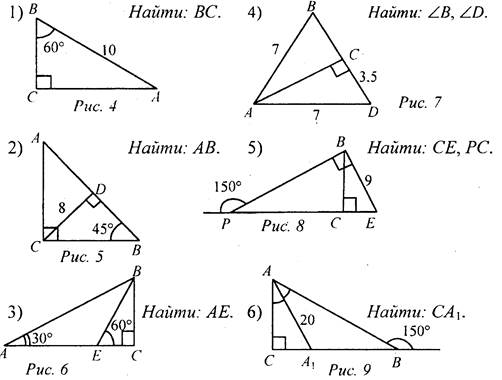
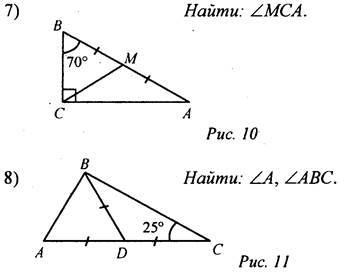
Решение: СН - высота. Пусть СН = х, тогда АВ = 4х. Проведем медиану СМ, В ΔСНМ ∠H = 90°, СН = х, СМ = 2х, тогда ∠HMC = 30°, следовательно, ∠AMC= 150°. ΔАМС - равнобедренный, тогда ∠A = ∠MCA = 15°. ΔАВС - прямоугольный, ∠A = 15°, тогда ∠B = 75°. Ответ: 15°, 75°. 2. Ответы для самопроверки. 1) ВС = 5. 2) АВ = 16. 3) АЕ = 14. 4) ∠B = ∠D = 60°. 5) СЕ = 4,5, PC = 13,5. 6) СА1 = 10. 7) ∠MCA = 20°. 8) ∠A = 65°, ∠ABC = 90° |
|||
|
III этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Какие свойства прямоугольного треугольника узнали на уроке? - Сформулируйте признак прямоугольного треугольника. - Оцените свою работу в группе. - Какие затруднения возникли? |
(И) Домашнее задание (дано на карточке): решить задачи.
|
||||