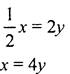Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РЕШЕНИЕ ЗАДАЧ - Урок 10 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для повторения и систематизации ранее изученного материала, выработки навыков решения задач; способствовать развитию логического мышления учащихся |
||
|
Термины и понятия |
Треугольник, противолежащий угол, катеты, гипотенуза |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, результаты, методы для решения задач |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения, работать в группе. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы |
• Задания для индивидуальной, групповой работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проанализировать ошибки, допущенные в самостоятельной работе |
(Ф/И) 1. Указать ошибки, допущенные в самостоятельной работе. 2. Решить задачи, вызвавшие затруднения у учащихся |
||
|
II этап. Устный опрос |
|||
|
Цель деятельности |
Задания для индивидуальной работы |
||
|
Привести в систему знания учащихся по теме “Прямоугольный треугольник” |
(Ф) К доске вызываются четверо учащихся, которые работают по карточкам (см. Ресурсный материал). Одновременно учитель проводит беседу с классом, задавая вопросы по теории |
||
|
III этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
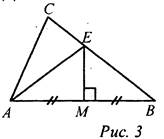
(Г) Организует деятельность учащихся: решение задач № 299 и 311. Дополнительная задача: Через середину стороны АВ треугольника АВС проведена прямая, перпендикулярная к АВ, пересекающая ВС в точке Е. ВС = 24 см, периметр треугольника АЕС равен 30 см. Найдите АС. Выполнив задание в группах, учащиеся представляют свои решения, обсуждают и записывают в тетрадях |
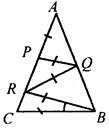
№ 299 Дано: АВ = АС, АР = PQ = QR = RB = ВС. Найти: ∠A.
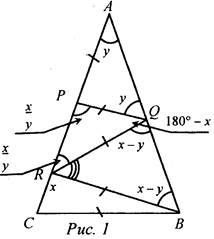
Решение: 1) Примем ∠C = ∠B = х, так как ΔАВС равнобедренный. Примем ∠CBR = y. Рассмотрим ΔRQB: ∠R + ∠Q + ∠B = 180°.
2) Рассмотрим ΔАВС: ∠А + ∠B + ∠C = 180°. 4у + 4у + у = 180° 9у = 180° у = 20° Ответ: ∠A = 20°. № 311
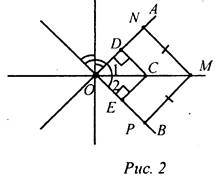
1) Проведем биссектрисы углов, образованных при пересечении двух прямых ОА и ОВ. Возьмем произвольную точку С на биссектрисе ∠AOB. ΔODC = ΔOEC по гипотенузе (ОС - общая гипотенуза) и острому углу (∠1 = ∠2), следовательно, CD = СЕ. 2) Проведем перпендикуляры MN и МР к прямым ОА и OB. ΔONM = ΔОРМ по катету и гипотенузе (ОМ - общая гипотенуза, MN = МР, так как по условию точка М равноудалена от сторон ОА и ОВ). Следовательно, ∠NOM = ∠POM, то есть луч ОМ - биссектриса ∠AOB. Из доказанных утверждений следует, что искомое множество точек состоит из двух прямых, содержащих биссектрисы углов, образованных при пересечении данных прямых. Дополнительная задача.
Решение: ΔАЕМ = ΔВЕМ по двум катетам, тогда АЕ = BE. РАBC = АС + АЕ + СЕ, но так как АЕ = BE, то PABC = АС + (BE + СЕ) = АС + СВ = АС + 24 = 30, отсюда АС = 6 см. Ответ: АС = 6 см |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какие цели были поставлены на уроке? Добились мы их? - Оцените свою работу и работу группы |
(И) Домашнее задание: повторить пункты 15-36; решить задачи № 266, 297; принести циркули и линейки |
||
Ресурсный материал
Карточки для индивидуальной работы
Вариант I
1. Сформулируйте теорему о сумме углов треугольника.
2. Один из углов при основании равнобедренного треугольника равен 65°. Найдите остальные углы треугольника.
3. В треугольнике ABC ∠B = 110°; биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.
Вариант II
1. Сформулируйте свойство катета прямоугольного треугольника, лежащего против угла в 30°.
2. В прямоугольном треугольнике ABC ∠C = 90°; ∠B = 60°, АВ = 15 см. Найдите ВС.
3. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.
Вариант III
1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.
2. В треугольниках ABC и A1B1C1 ∠B = ∠B1 = 90°; АВ = А1В1, АС = А1С1. Найдите углы А1 и С1 треугольника А1В1С1, если ∠A = 34°, ∠C = 54°.
3. На сторонах угла А отмечены точки В и С так, что АВ = АС. Через точки В и С проведены прямые, перпендикулярные соответственно сторонам АВ и АС данного угла и пересекающиеся в точке М. Докажите, что МВ = МС.
Вариант IV
1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу.
2. В треугольниках АВС и А1В1С1 углы В и В1 прямые, ∠A = ∠A1, АС = А1С1. Найдите стороны В1С1 и А1В1 треугольника А1В1С1, если ВС = 17 см, АВ = 12 см.
3. Даны два равных прямоугольных треугольника АВС и А1В1С1, у которых ∠B = ∠B1 = 90°; ВН и В1Н1 - высоты. Докажите, что ΔВНС = ΔВ1Н1С1.