РЕШЕНИЕ ЗАДАЧ - Урок 11 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цели деятельности учителя

Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки

Термины и понятия

Угол, окружность, дуга окружности, отрезок

Планируемые результаты

Предметные умения

Универсальные учебные действия

Имеют систематические знания о плоских фигурах и их свойствах, владеют умением применять систематические знания o них для решения геометрических и практических задач

Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.

Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы.

Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Деятельность учителя

Деятельность учащихся

Систематизировать полученные знания

(Ф/И)

1. Ответить на вопросы учащихся по выполнению домашнего задания.

2. Организовать решение задач № 285, 291 (д) с последующим обсуждением (дать учащимся на каждую задачу 2-3 минуты; решение записывается в тетрадях и на доске)

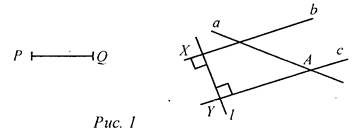
№ 285.

Построение:

1) Построим прямую l, перпендикулярную прямой b и проходящую через произвольную точку X прямой b.

2) Отложим от точки X на прямой l отрезок XY, равный PQ.

3) Построим прямую с, перпендикулярную прямой l и проходящую через точку Y.

4) Точку пересечения а и с обозначим А. Точка А прямой а удалена от прямой b на расстояние PQ, то есть А - искомая точка.

Задача имеет два решения: отрезок XY на прямой l можно отложить в разные стороны от прямой b.

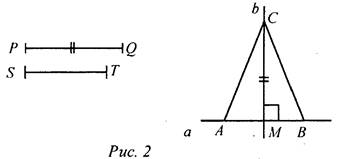
№ 291 (д).

Дано: медиана PQ, проведенная к основанию; основание равнобедренного треугольника ST.

Построение:

Так как медиана, проведенная к основанию равнобедренного треугольника, является его высотой, то ход построения будет следующим:

1) На прямой а отложим отрезок АВ, равный ST.

2) Построим середину отрезка АВ - точку М

3) Через точку М построим прямую b, перпендикулярную прямой а, и отложим на этой прямой b от точки М отрезок МС, равный PQ.

4) Соединим точки А и С, В и С отрезками. ΔАВС - искомый.

Задача имеет два решения: на прямой b от точки М можно отложить два отрезка, равных PQ.

II этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Изучить новый материал

(Ф/И)

1. Разобрать решение задачи № 3 на доске и в тетрадях (с. 84-85).

2. Построить треугольник по трем сторонам (рис. 141 и решение задачи на с. 85 учебника). Провести исследование, всегда ли задача № 3 имеет решение

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки в решении задач

(Ф/И) Организует деятельность учащихся: решение задач № 289, 290, 292 на доске и в тетрадях

№ 289.

Дано:

Построить ΔAВС: АВ = PQ, ∠A = hk, ∠B = 1/2h₁k₁.

Анализ:

Ход построения:

1) Отрезок АВ = PQ;

2) ∠A = hk;

3)

4) стороны ∠A и ∠B пересекаются в точке С;

5) ΔАВС - искомый.

№ 290.

а) Дано:

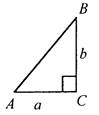
Построить ΔАВС: ∠C = 90°, АС = а, СВ = b.

Анализ:

Ход построения:

1) Построить прямой угол С;

2) на одной стороне отложить отрезок АС = а, а на другой - СВ = b;

3) соединить отрезком А и В;

4) ΔАВС - искомый.

б) Дано:

Построить ΔАВС: ∠C = 90°, ∠A = а, АС = а.

Анализ:

Ход построения:

1) Построить прямой угол С;

2) отложить на стороне угла АС = а;

3) построить ∠A = а;

4) стороны ∠A и ∠C пересекаются в точке В;

5) ΔАВС - искомый.

№ 292.

Дано:

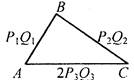
а) Построить ΔАВС: АВ = P₁Q₁, ВС = P₂Q₂, АС = 2P₃Q₃.

Анализ:

Ход построения:

1) Отрезок АВ = P₁Q₁;

2) окружность с центром А и R = P₂Q₂;

3) окружность с центром В и R = 2P₃Q₃;

4) эти две окружности пересекаются в точке С;

5) ΔАВС - искомый.

б) Построить ΔАВС: АВ = 2P₁Q₁, ВС = P₂Q₂, АС = 3/2P₃Q₃.

Анализ:

Ход построения:

1) ВС = P₂Q₂,

2) окружность с центром В и R = 2P₁Q₁;

3) окружность с центром С и R = 3/2P₃Q₃;

4) окружности пересекаются в точке A;

5) ΔАВС - искомый.

Указание: нужно помнить, что сумма длин двух сторон треугольника должна быть больше длины третьей стороны

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке.

- Закончите фразы:

• Я познакомился с...

• Было непросто...

• Я добился...

• У меня получилось...

• Хотелось бы...

• Мне запомнилось...

• Я попробую...

(И) Домашнее задание: пункты 38-39; вопросы 14-20 на с. 89; решить задачи № 273, 287, 288, 291 (а, б, г), 293 (разобрана в учебнике на с. 87-88)