Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ПОВТОРЕНИЕ. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для приведения в систему знаний, умений, навыков по теме “Соотношения между сторонами и углами треугольника”; совершенствовать навыки решения задач |
||||
|
Термины и понятия |
Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Задания для математического диктанта. • Тест |
||||
|
I этап. Актуализация опорных знаний учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Ситематизировать теоретические знания |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Математический диктант с взаимопроверкой. Тексты раздаются каждому учащемуся. На работу дается 3 минуты. После этого на экран выводятся правильные ответы. - Закончите предложения. • Сумма углов треугольника равна ... • Треугольник, у которого есть прямой угол, называется ... • Гипотенузой прямоугольного треугольника называется ... другие стороны называются ... • Треугольник, в котором все три угла острые, называется ... • Треугольник, в котором один угол тупой, называется ... • Угол, смежный с внутренним углом треугольника, называется ... • Внешний угол треугольника равен ... • В треугольнике против большего угла лежит ... сторона, а против большей стороны лежит ... угол. • В прямоугольном треугольнике ... больше катета. • Если два угла треугольника равны, то треугольник ... • Каждая сторона треугольника меньше ... • Сумма двух острых углов прямоугольного треугольника равна ... • Катет прямоугольного треугольника ... равен половине гипотенузы. • Если катет прямоугольного треугольника ... то угол ... равен 30° |
||||
|
II этап. Тест |
|||||
|
Цель деятельности |
Тестовые задания |
||||
|
Проверить умение применять теоретические знания в решении задач |
(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал). Методические указания: Время на выполнение - 35-40 минут (если часть 3 не предлагается, то время уменьшить до 20-25 минут). Нормы отметок: “5” - 18-20 баллов; “4” - 15-17 баллов; “3” - 11-14 баллов; “2” - 0-10 баллов. Рекомендации по оцениванию решения задания С1 части 3: |
||||
|
Баллы |
Критерии оценки |
||||
|
5 |
Приведена верная последовательность всех шагов решения. Обоснованы все ключевые моменты. Проведены верные вычисления. Получен верный ответ |
||||
|
4 |
Имеются все шаги решения. Использованы правильно теоремы, получен правильный ответ. В решении есть негрубые вычислительные ошибки или не обоснованы некоторые из ключевых моментов |
||||
|
3 |
Имеется более половины шагов решения задачи, найдены некоторые из искомых величин |
||||
|
2 |
Ход решения задачи правильный, но выполнено менее половины решения задачи |
||||
|
1 |
Выполнен один из шагов приведенного возможного варианта решения |
||||
|
0 |
Решение задачи отсутствует |
||||
|
III этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Оцените свою работу на уроке и работу своего товарища |
(И) Домашнее задание: решить № 335 |
||||
Ресурсный материал
Тест
Часть 1
A1. Тупоугольный треугольник изображен на рисунке:

А2. Гипотенузой треугольника АВС, изображенного на рисунке, является сторона...
а) АВ;
б) ВС;
в) АС;
г) АВ и АС.

А3. В треугольнике MNK наибольшей стороной является...
a) MN;
б) МК;
в) KN;
г) MK и МN.

А4. Равнобедренным является треугольник, изображенный на рисунке...

А5. Две стороны треугольника равны 2 см и 3 см. Тогда третья сторона треугольника может быть равна...
а) 6 см;
б) 5 см;
в) 3 см;
г) 1 см.
А6. В треугольнике MNK один из углов тупой. Другие два угла треугольника могут быть...
а) только острыми;
б) один острым, другой прямым;
в) один тупым, другой острым;
г) один прямым, другой тупым.
Часть 2
В1. На рисунке прямоугольными являются треугольники __________________________________

В2. Меньшей стороной треугольника АВС является __________________________________

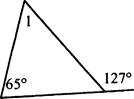
В3. На рисунке ∠1 = __________________________________
В4. Величина одного из углов равнобедренного треугольника равна 70°. Тогда другие углы треугольника будут равны __________________________________
В5. На рисунке ∠ABE = 104°, ∠ACB = 76°, АС = 12 см. Тогда сторона АВ треугольника АВС будет равна ______________________________________________________

В6. В равностороннем треугольнике АВС проведены биссектрисы AD и BF, которые пересекаются в точке О. Тогда углы треугольника AOF будут равны __________________________________
В7. На чертеже величина угла С равна __________________________________
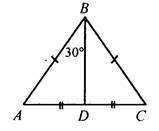
В8. В треугольнике АВС медиана BD в 2 раза меньше стороны АС. Угол В треугольника АВС равен __________________________________
В9. В треугольнике AВС угол А больше угла В на 40°, а угол С меньше угла A на 20°. Тогда ∠В = __________________________________
Часть 3
СКВ треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок CD, равный СВ. Найдите углы треугольника ABD.
Ответы:
Часть 1
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
|
а |
б |
в |
г |
в |
а |
Часть 2
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
В8 |
В9 |
|
KMN, HSL |
ВС |
62° |
70°, 40° или 55°, 55° |
12 см |
30°, 30°, 120° |
60° |
90° |
40° |
Часть 3
Возможный вариант оформления решения задачи.
С1.
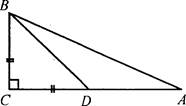
1. Так как в треугольнике АВС сумма углов равна 180°, то ∠А = 20°.
2. Так как ВС = CD, то прямоугольный треугольник BCD является равнобедренным, поэтому ∠CBD = ∠CDB = 45°.
3. Углы BDC и ADB являются смежными, а так как сумма смежных углов равна 180°, то ∠BDA = 135°.
4. В треугольнике ABD: ∠BDA = 135°, ∠DAB = 20°, поэтому ∠ABD = 25°.
5. Таким образом, углы треугольника ABD будут равны: ∠BDA = 135°, ∠DAB = 20°, ∠ABD = 25°.