ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ - НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ

Цели деятельности учителя

Создать условия для повторения понятия перпендикулярных прямых, рассмотрения свойства перпендикулярных прямых; совершенствовать у учащихся умение решать задачи

Термины и понятия

Угол, смежные углы, вертикальные углы, перпендикулярные прямые

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные ресурсы

• Чертежи к задачам.

• Задания для парной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Систематизировать теоретическиезнания

(Ф/И)

1. Обсуждение вопросов учащихся по домашнему заданию.

2. Выполнение задания: на каком рисунке изображены смежные углы?

II этап. Решение задач по готовым чертежам

Цель деятельности

Совместная деятельность

Совершенствовать навыки решения задач

(П) Выполнение заданий и взаимопроверка.

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие перпендикулярных прямых

(Ф/И)

При изучении нового материала можно опираться на имеющиеся у учащихся знания по данной теме за курс математики 6 класса.

- Какие прямые называются перпендикулярными? (Две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.)

- Запишите, используя математические символы: “Прямая АВ перпендикулярна прямой CD”. Выполните соответствующий рисунок и укажите все углы.

- Пересекаются ли две прямые, перпендикулярные третьей? (Нет.)

Учащиеся могут вспомнить, что такие прямые параллельны.

- Две прямые, перпендикулярные третьей, не пересекаются - это свойство перпендикулярных прямых. Докажем это свойство (п. 12 учебника). (Доказывает учитель.)

П. 13 “Построение прямых углов на местности” можно порекомендовать прочитать дома

IV этап. Решение задач

Цель деятельности

Совместная деятельность

Совершенствовать навыки решения задач по изученной теме

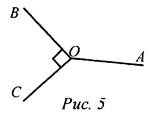
(П) После выполнения заданий представить решение задач на доске.

№ 1.

Два тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны.

Найдите величину тупых углов, если известно, что они равны.

Решение:

∠AOB = ∠AOC. ВО ⊥ ОС, значит, ∠BOC = 90°.

Так как ∠AOB = ∠AOC, то 2∠AOB = 360° - 90° = 270°, ∠AOB = 135°.

№ 2.

Из вершины развернутого угла проведены два луча, которые делят его на три равные части.

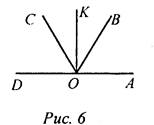
Решение:

∠AOB = ∠BOC = ∠COD = 60°. OK - биссектриса ∠BOC, тогда ∠COK = ∠BOK = 30°, следовательно, ∠DOK = 60° + 30° = 90°, ∠AOK = 60° + 30° = 90°, то есть OK ⊥ OA, OK ⊥ OD.

№ 3.

Углы AOB и DOC смежные, ОМ - биссектриса ∠AOB, луч ON принадлежит внутренней области ∠BOC и перпендикулярен ОМ. Является ли ON биссектрисой ∠BOC? Почему?

Решение:

∠AOB и ∠BOC смежные, значит, ∠AOB = 180° - ∠BOC, а так как ОМ - биссектриса ∠AOB, то ∠BOM = ∠MOA = 1/2(180° - ∠BOC) = 90° - 1/2∠BOC. Так как ON ⊥ ОМ, то ∠MON = 90°, a ∠BOM = 90° - ∠BON. Получили, что ∠BOM = 90° - 1/2∠BOC = 90° - ∠BON, откуда следует, что 1/2∠BOC = ∠BON, то есть ON является биссектрисой ∠BOC

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке и работу своих товарищей.

- Что нового узнали на уроке?

(И) Домашнее задание: решить задачи № 66, 68 и дополнительные задачи.

1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.

2. Сумма трех углов, образовавшихся при пересечении двух прямых, равна 325°. Найдите остальные углы