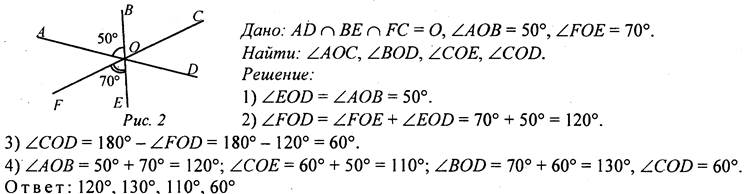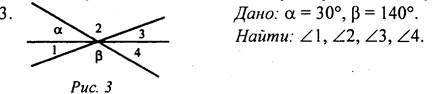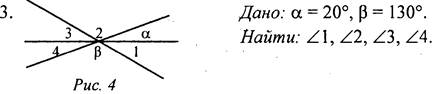Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РЕШЕНИЕ ЗАДАЧ - НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ
|
Цель деятельности учителя |
Создать условия для повторения, закрепления материала главы I; совершенствовать навыки решения задач; подготовить учащихся к предстоящей контрольной работе |
|||
|
Термины и понятия |
Угол, смежные углы, вертикальные углы, перпендикулярные прямые, биссектриса угла, луч, отрезок |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок: осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для самостоятельной работы. • Тест |
|||
|
I этап. Актуализация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) Проверка домашнего задания. К доске вызываются двое учащихся. № 66.
№ 68.
|
|||
|
II этап. Самостоятельная работа |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Проверить уровень сформированности знаний при решении простейших задач |
(И) Работа рассчитана на 10-15 минут. Далее осуществляется взаимопроверка. Вариант I 1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы. 2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.
Вариант II 1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы. 2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы.
Решение: Вариант I
Так как ∠1 : ∠2 = 1 : 2, то ∠1 = x, ∠2 = 2х. Но ∠1 + ∠2 = 180°, тогда х + 2х = 180°, х = 60, значит, ∠1 = 60°, ∠2 = 120°.
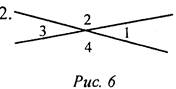
Пусть ∠1 = 21°, тогда ∠3 = ∠1, как вертикальные, и ∠3 = 21°. ∠1 и ∠2 - смежные и ∠1 + ∠2 = 180°. Тогда ∠2 = 180° - ∠1 = 159°. Но ∠2 = ∠4, как вертикальные, значит, ∠4 = 159°. 3. а = 30°, тогда ∠4 = 30°, так как ∠4 и угол с градусной мерой а – вертикальные, β = 140°, тогда ∠2 = 140°, так как ∠2 и угол с градусной мерой β - вертикальные. ∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180° - (∠2 + ∠4) = 10°. ∠3 и ∠1 - вертикальные, поэтому ∠3 = ∠1, ∠1 = 10°. Вариант II
∠2 на 20° больше ∠1, тогда ∠1 = х, ∠2 = х + 20°. Но ∠1 + ∠2 = 180°, тогда х + х + 20° = 180°, х = 80°, значит, ∠1 = 80°, ∠2 = 100°.
Пусть ∠1 = 102°, тогда ∠3 = ∠1, как вертикальные, и ∠3 = 102°. ∠1 и ∠2 - смежные и ∠1 + ∠2 = 180°, тогда ∠2 = 180° - ∠1 = 78°. Но ∠2 = ∠4, как вертикальные, значит, ∠4 = 78°. 3. а = 20°, тогда ∠4 = 20°, так как ∠4 и угол с градусной мерой а – вертикальные, β = 130°, тогда ∠2 = 130°, так как ∠2 и угол с градусной мерой β - вертикальные. ∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180°- (∠2 + ∠4) = 30°. ∠3 и ∠1 - вертикальные, поэтому ∠3 = ∠1, ∠1 = 30° |
|||
|
III этап. Тест |
||||
|
Цель деятельности |
Тестовые задания |
|||
|
Повторить теоретический материал |
(И) 1. Точка С лежит на луче АВ. Какая из точек А, В, С лежит между двумя другими? а) А; б) В или С; в) С; г) В. 2. Отрезок ХМ пересекает прямую а. Отрезок XD пересекает прямую а. Пересекает ли прямую а отрезок MD? а) Да; б) может не пересекать; в) никогда не пересекает; г) нет правильного ответа. 3. Один из углов, образованных при пересечении двух прямых, - прямой. Остальные углы... а) острые и прямой; б) тупые и прямой; в) прямые; г) нет правильного ответа. 4. Сумма двух углов, образованных при пересечении двух прямых, равна 180°. Эти углы... а) смежные; б) вертикальные; в) нет правильного ответа; г) могут быть смежными, могут быть вертикальными. 5. Если точка В принадлежит отрезку АС, то... а) АВ + ВС = АС; б) АВ + АС = ВС; в) ВС + АС = АВ; г) нет правильного ответа. 6. Если луч ОС проходит между сторонами угла АОВ, то... а) ∠AOC = ∠BOC; б) ∠AOC + ∠BOC = ∠AOB; в) ∠AOB + ∠BOC = ∠AOC; г) ∠AOC + ∠AOB = ∠BOC. 7. Если точка В - середина отрезка АС, то... а) АВ + ВС = АС; б) АС = ВС; в) АВ = 2АС; г) АС = 2АВ. 8. Если луч ОС - биссектриса ∠AOB, то... а) ∠AOB = ∠AOC + ∠BOC; б) ∠AOC = ∠AOB; в) ∠AOC = ∠BOC; г) ∠AOB ≠ ∠BOC. Ответы: 1 - б; 2 - г; 3 - в; 4 - г; 5 - а; 6 - б; 7 - г; 8 - в |
|||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Оцените свою работу на уроке. - Какие понятия повторяли на уроке? |
(И) Домашнее задание: решить задачи № 74, 75, 80, 82 |
|||