ПЛОЩАДЬ МНОГОУГОЛЬНИКА - ПЛОЩАДЬ

Цель деятельности учителя

Создать условия для представления об измерении площадей многоугольников, рассмотрения основных свойств площадей и выведения формулы для вычисления площади квадрата

Термины и понятия

Равновеликие многоугольники, равносоставленные многоугольники

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях

Познавательные: умеют выбирать и создавать алгоритмы для решения математических проблем.

Регулятивные: умеют самостоятельно ставить цели, адекватно оценивать правильность или ошибочность выполнения учебной задачи.

Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Учебник.

• Задания для фронтальной и индивидуальной работы

I этап. Анализ ошибок, допущенных в контрольной работе

II этап. Подготовка к восприятию нового материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Подготовить учащихся к восприятию понятия площади многоугольника

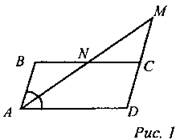
(Ф) Решить задачи:

1. Через точку во внутренней области равностороннего треугольника проведены две прямые, параллельные двум сторонам треугольника. На какие фигуры разбивается этими прямыми данный треугольник?

2. Дано: ABCD - параллелограмм, AD = 2АВ, AM - биссектриса ∠BAD. Докажите, что часть отрезка AM,лежащая во внутренней области параллелограмма ABCD, равна части, лежащей во внешней области

Доказать: AN = NM.

Доказательство:

1. ∆ABN -равнобедренный (АВ =BN).

2. ∠DAN = ∠ANB (накрест лежащие); ∠ANB = ∠MNC(вертикальные).

3. Так как AD = 2АВ, тоBN = NC.

4. ∠ABN = ∠MCN (накрест лежащие).

5. ∆ABN = ∆MCN (по II признаку), значит, AN =NM

III этап. Изучение новой темы

Цель деятельности

Совместная деятельность

Ввести понятие площади многоугольника

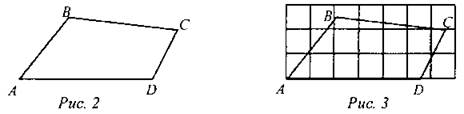
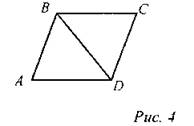
(Ф) 1. Ввести понятие площади.

- Понятие площади каждому известно из жизненного опыта. Часто мы слышим: “площадь нашей квартиры равна 60 м²”.

Как вы понимаете это предложение? (Это величина квартиры. Пол данной квартиры можно застелить 60 квадратами со стороной 1 м.)

- С сегодняшнего дня мы будем учиться вычислять площади различных геометрических фигур.

2. Определить единицы измерения площадей.

- Как и измерение длин отрезков, измерение площадей проводится с помощью единиц измерения. Какие единицы измерения площадей вам известны? (Квадратный метр - м²; квадратный сантиметр - см²; квадратный миллиметр - мм²; ар (сотка) - 100 м²; га (гектар) - 10 000 м², и др.)

- Как вы понимаете утверждение “единица измерения площади см²”? (Площадь измеряется квадратами со стороной 1 см.)

- Может ли площадь фигуры выражаться отрицательным числом? (Нет, не может.)

3. Дать представление об измерении площадей многоугольников способом разбиения фигуры на квадраты.

- Как измерить площадь фигуры, изображенной на рис. 2 в квадратных дециметрах? (Нужноразбить фигуру на квадратные дециметры.)

- Сторону AD разобьем на отрезки по 1 дм каждый и через концы отрезков проведем прямые, перпендикулярные стороне AD.Далее проведем прямые, параллельные AD, на расстоянии 1 дм друг от друга (рис. 3.). Сосчитаем количество целых квадратов, вместившихся в фигуру ABCD. Неполные квадраты разобьем на квадратные сантиметры. Каждый квадратный сантиметр - это сотая часть квадратного дециметра. Таким образом, можно вычислить площадь фигуры в дм² с точностью до 0,01 дм². Для более точного измерения площади данной фигуры неполные квадраты со стороной 1 см разобьем на квадраты со стороной 1 мм, и т. д.

- Такой способ вычисления площадей фигур называется способом разбиения фигуры на квадраты. Но чаще всего площади геометрических фигур вычисляются по готовым формулам, с которыми мы познакомимся на следующих уроках.

4. Рассмотреть свойства площадей.

а) Равные многоугольники имеют равные площади.

б) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

в) Площадь квадрата равна квадрату его стороны. (Доказательство третьего свойства является трудным, поэтому п. 49 можно предложить более подготовленным учащимся изучить самостоятельно.)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

На примере устных задач и простых задачах отработать

понятие площади

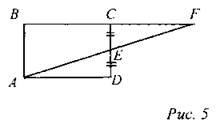
(Ф/И) Решите задачи (устно):

1. ABCD - параллелограмм.

S_ABCD = 12.

Найти: S_ABD, S_BCD.

2. ABCD - прямоугольник.

СЕ = DE, S_ABCD = Q.

Найти: S_ABF.

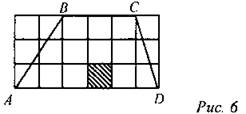
3. Площадь заштрихованного квадрата равна 1.

Найти: S_ABCD.

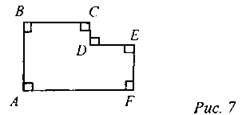
4. АВ = ВС = 3, AF = 5, EF = 2.

Найти: S_ABCDEF.

5. Решить на доске и в тетради № 449 (в), 450 (в). К доске вызываются двое учеников. После выполнения заданий осуществляется проверка.

6. Самостоятельно решить № 449 (а), 450 (а), 451, 447

1. 6 и 6.

2. S_ABCD = Q.

3. 13,5.

4. 9 + 4 = 13.

№ 449 (в).

a = 3√2, S = a = (3√2) ∙ 2 = 18 (м²).

№ 450 (в).

S = 12, а = √12 = 2√3 (м).

№ 449 (а). 1,44 см².

№ 450 (а). 4 см.

№ 451 (а). 24 см² = 24 ∙ 100 мм² = 2400 мм².

№ 451 (б). 24 см² = 24 ∙ 0,01 дм² = 0,24 дм²

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Составьте синквейн к уроку.

- Что нового узнали на уроке?

(И) Домашнее задание: п. 49, вопросы 1, 2; решить задачи № 448, 449 (б), 450 (б), 446