ПАРАЛЛЕЛОГРАММ. СВОЙСТВА ПАРАЛЛЕЛОГРАММА - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для введения определения параллелограмма и его свойств

Термины и понятия

Параллелограмм, противолежащие стороны, противолежащие углы

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, какой многоугольник называется параллелограммом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии

Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи; понимают и используют наглядность для иллюстрации примеров, интерпретации математических фактов, аргументации собственного суждения.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности; осуществляют планирование и контроль.

Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для самостоятельной работы

I этап. Проверка домашнего задания

Цель деятельности

Совместная деятельность

Выявить трудности у учащихся при выполнении домашней работы

Обсудить выполнение домашней работы (решение задач), ответить на вопросы учащихся

II этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Выявить у учащихся умение находить сумму углов многоугольников

(И)

Вариант I

1. Найдите сумму углов выпуклого тринадцатиугольника. (1980°.)

2. Каждый угол выпуклого многоугольника равен 135°. Найдите число сторон этого многоугольника. (8.)

Вариант II

1. Найдите сумму углов выпуклого двенадцатиугольника. (1800°.)

2. Сумма углов выпуклого многоугольника с равными углами равна 1260°. Найдите число сторон этого многоугольника. (9.)

Вариант III (для более подготовленных учащихся)

Каждый угол данного выпуклого многоугольника равен 150°. Найдите сумму углов выпуклого многоугольника, число сторон которого в два раза меньше, чем число сторон данного многоугольника, ((n - 2) ∙ 180° = 150n; n = 12 - число сторон исходного многоугольника; 6 сторон у второго многоугольника. Сумма его углов 720°)

III этап. Учебно-познавательная деятельность

Изучение нового материала

Цель деятельности

Совместная деятельность

Дать определение параллелограмма и доказать его свойства

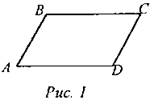
(Ф/И) 1. Дать определение параллелограмма. Воспроизвести рис. 157 из учебника (один r с учащийся - на доске, остальные - в тетрадях) и сделать запись: “Параллелограмм ABCD”. Предложить учащимся записать пары параллельных сторон: АВ || СD, ВС || AD.

(Ф) 2. Рассмотреть свойства параллелограмма:

• В параллелограмме противоположные стороны и противоположные углы равны.

• Диагонали параллелограмма точкой пересечения делятся пополам.

(Ф) 3. Доказать любое свойство параллелограмма в классе, на дом предложить доказательство второго свойства

Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Закрепить полученные знания

(Ф/И)

1. Докажите, что сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

2. Решите задачи № 376 (а) (устно); № 376 (б), 372 (а).

№ 376 (а). ∠А = ∠C = 84°, ∠B = ∠D = 180° - 84° = 96°.

№ 376 (б). Можно решить системой уравнений:

∠A - ∠B = 55°; ∠A + ∠B = 180°; ∠A = 117,5°, ∠B = 62,5°

№ 372 (а). Пусть одна сторона х см, тогда вторая (х + 3) см. Так как периметр равен 48 см, то составим и решим уравнение: (х + х + 3) ∙ 2 = 48; х = 10,5; таким образом, одна сторона равна 10,5 см, вторая - 13,5 см

IV этап. Итоги урока

Цель деятельности

Деятельность учителя

Деятельность учащихся

Подвести итог изученному теоретическому материалу

(Ф) Если в условии задачи дано, что ABCD - параллелограмм, то можно использовать его свойства:

АВ || CD, ВС || AD; АВ = CD, ВС = AD; ∠А = ∠C, ∠В = ∠D; ∠А + ∠В = 180° и т. д.; АО = ОС, BO =OD.

V этап. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И) Составьте синквейн к уроку

(И) Домашнее задание: вопросы 6-8, с. 113; № 372 (б), 376 (в, г), 374; доказать одно из свойств параллелограмма (то, которое в классе не доказывали)