ВЫПУКЛЫЙ МНОГОУГОЛЬНИК - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для выведения формулы суммы углов выпуклого многоугольника, решения задачи с помощью выведенной формулы, повторения признаков параллельности прямых и свойств углов при параллельных прямых и секущей при решении задач

Термины и понятия

Выпуклый, невыпуклый многоугольник; сумма углов многоугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, что такое ломаная, многоугольник, его вершины, смежные стороны, диагонали; изображают и распознают многоугольники на чертежах; показывают элементы многоугольников, внутреннюю и внешнюю области многоугольников; формулируют и доказывают утверждение о сумме углов выпуклого многоугольника

Познавательные: проводят информационно-смысловой анализ текста и лекции; осмысливают ошибки и устраняют их.

Регулятивные: понимают смысл поставленной задачи.

Коммуникативные: выстраивают аргументацию, участвуют в диалоге, приводят примеры и контрпримеры.

Личностные: проявляют критичность мышления; распознают логически некорректные высказывания

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для парной и фронтальной работы

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Повторить основные элементы треугольника

(Ф) 1. Какая фигура называется четырехугольником?

2. Какие вершины многоугольника называются соседними? Какие - противоположными?

3. Что такое диагонали многоугольника? Напомнить учащимся определение треугольника. Вспомнить элементы треугольника (сторона, вершина, угол)

II этап. Учебно-познавательная деятельность

Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Вывести формулу суммы углов многоугольника

(П/Ф) 1. Чему равна сумма углов выпуклого пятиугольника? (Возникает проблемная ситуация.)

Изучение нового материала

Цель деятельности

Совместная деятельность

Вывести формулу суммы углов многоугольника

- Как зависит сумма углов многоугольника от числа треугольников, на которые он разбивается диагоналями, проведенными из одной вершины?

Многоугольник

1

2

3

4

Число углов

3

4

5

6

Число треугольников

1

2

3

4

Сумма углов

180°

360°

540°

720°

Значит, сумма внутренних углов n-угольника равна 180° ∙ (n - 2), где n - число сторон многоугольника. Сумма внешних углов n-угольника не зависит от количества сторон и всегда равна 360°. Объясните: почему?

Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Закрепить полученные знания

(Ф) 1. Найдите сумму углов выпуклого:

а) восьмиугольника;

б) двенадцатиугольника.

(Ф) 2. Сколько сторон имеет выпуклый многоугольник, если его сумма углов равна 2340°?

(И) 3. Решить № 364 (в), 365

1. а) n = 8; (8 - 2) ∙ 180°= 1080°.

б) n = 12; (12 - 2) ∙ 180° = 1800°.

2. (n - 2) ∙ 180 = 2340

n - 2= 13

n = 15

Ответ: многоугольник имеет 15 сторон.

№ 364.

в) n = 10; (10 - 2) ∙ 180° = 1440°

№ 365.

а) α = 90°; (n - 2) ∙ 180° = 90° n; n = 4

б) α = 60°; (n - 2) ∙ 180° = 60° n; n = 3

в) α = 120°; (n - 2) ∙ 180° = 120° n; n = 6

г) α = 108°; (n - 2) ∙ 180° = 108° n; n = 5

III этап. Повторение

Цель деятельности

Деятельность учителя

Деятельность учащихся

Повторить изученный материал

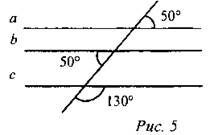
(Ф) 1. Параллельны ли прямые а, b и с?

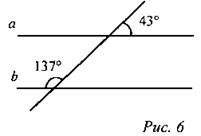
(Ф) 2. Параллельны ли прямые а и b?

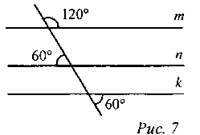
(Ф) 3. Параллельны ли прямые m и n, n и k, m и k?

1. Параллельны.

2. Да.

3. Да

IV этап. Итоги уhока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали на уроке?

- Какой этап урока оказался для вас самым сложным?

- Оцените свою работу на уроке