РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛОГРАММ» - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для закрепления знаний о свойствах и признаках параллелограмма в процессе решения задач

Термины и понятия

Выпуклый, невыпуклый многоугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии

Познавательные: умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи; воспринимают устную речь; проводят информационно-смысловой анализ текста и лекции; осмысливают ошибки и устраняют их.

Регулятивные: понимают смысл поставленной задачи.

Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.

Личностные: выражают интерес к изучению предметного курса; проявляют готовность и способность к саморазвитию; имеют мотивацию к обучению и познанию

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для работы по индивидуальным карточкам, для самостоятельной работы по вариантам, для парной работы

I этап. Актуализация опорных знаний

Цель деятельности

Задания для самостоятельной работы

Повторить основные свойства и признаки параллелограмма

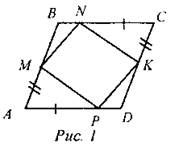
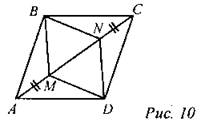
(И) Работа по индивидуальным карточкам (3-6 человек).

1-й уровень.

1. Точки Е и К- середины сторон АВ и CD параллелограмма ABCD. Докажите, что АЕСК - параллелограмм.

2. Диагонали четырехугольника ABCD пересекаются в точке О, причем АС = 2 дм, АО = 10 см, BD = 1,5 дм, ВО = 1 см. Выясните, является ли ABCDпараллелограммом.

2-й уровень.

1. В параллелограмме ABCD на сторонах АВ и CD отмечены соответственно точки М и N так, что ∠ВМС = ∠AND. Докажите, что AMCN - параллелограмм.

2. Точки А и В делят диагональ МК параллелограмма MNKP на три равные части. Является ли четырехугольник ANBP параллелограммом? Ответ обоснуйте.

3-й уровень.

Дано: ABCD - параллелограмм, AM = СК, АР = CN (рис. 1).

Доказать: MNKP - параллелограмм.

(И) Остальные учащиеся выполняют самостоятельную работу по вариантам.

Вариант I

1. В четырехугольнике ABCD АВ || CD и АВ = CD, АС = 10 см, BD = 5 см, АВ = 6,5 см. Диагонали четырехугольника пересекаются в точке О. Найти периметр треугольника COD.

2. В параллелограмме ABCD из вершины В тупого угла АВС проведен перпендикуляр ВК к стороне AD (К є AD) и ВК = 0,5АВ. Найти углы параллелограмма.

Вариант II

1. В четырехугольнике ABCD О - точка пересечения диагоналей и ВС = AD, АВ = CD, АС = 16 см, BD = 14 см, Р_∆AOB = 25 см. Найти АВ.

2. В параллелограмме ABCD из вершины В тупого угла опущен перпендикуляр ВК на сторону AD и АК = ВК. Найти углы параллелограмма

II этап. Решение задач по готовым чертежам

Цель деятельности

Деятельность учителя

Деятельность учащихся

Повторить основные свойства и признаки параллелограмма

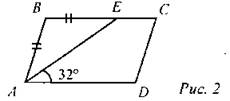
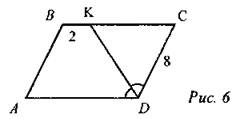
(П)

1. ABCD - параллелограмм.

Найти: ∠С, ∠D.

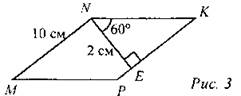
2. MNKP - параллелограмм.

Найти: МР, РК.

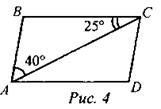
3. Найти углы параллелограмма ABCD.

4. ABCD - параллелограмм.

Найти: P_ABCD.

5. ABCD - параллелограмм.

Найти: AD.

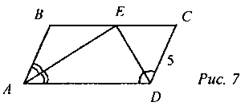
6. ABCD - параллелограмм.

Найти: P_ABCD, ∠AED.

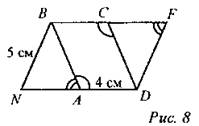
7. NBFD - параллелограмм. AD = 4 см, NB = 5 см.

Найти: ВС, CD.

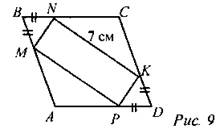
8. ABCD - параллелограмм. PMNKP = 20 см.

Найти: MN, МР.

9. BNDM - параллелограмм. АВ : ВС = 4 : 5, P_ABCD = 18 см.

Найти: AD, DC.

1. ∠С = 64°, ∠D = 116°.

2. МР = 4 см, РК = 10 см.

3. ∠B = ∠D = 115°, ∠A = ∠C = 65°.

4. P_ABCD= 16см.

5. AD = 10 см.

6. P_ABCD = 30 см, ∠AED = 90°.

7. BC = 4 см, CD = 5 см.

8. MN = 3 см, МР = 1 см.

9. AD = 5 см, DC = 4 см

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие свойства и признаки параллелограмма повторили на уроке?

- Оцените свою работу на уроке

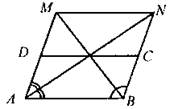
(И) Домашнее задание: разобрать по учебнику № 385 (Теорему Фалеса), решить задачу:

Дано: ABCD - параллелограмм. AN -биссектриса ∠BAD, ВM - биссектриса ∠АВС.

Доказать: ABNM-параллелограмм.