РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛОГРАММ. ТРАПЕЦИЯ» - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для закрепления понятий “трапеция”, “равнобокая трапеция”, “прямоугольная трапеция”; для рассмотрения решения задач, в которых раскрываются свойства трапеции

Термины и понятия

Трапеция, основания трапеции, боковые стороны, параллелограмм, свойства, признаки

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, какой многоугольник называется трапецией, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии

Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи.

Регулятивные: принимают и сохраняют учебную задачу.

Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе.

Личностные: умеют контролировать процесс и результат учебной математической деятельности

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для фронтальной, индивидуальной, парной работы

I этап. Проверка домашнего задания

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при выполнении заданий домашней работы; проверить уровень усвоения теоретического материала

(Ф) 1. Дайте определение трапеции.

2. Какие виды трапеций существуют?

3. Перечислите свойства равнобедренной трапеции

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Создать условия для применения теоретических знаний при решении задач

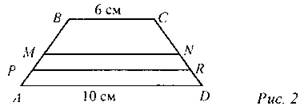
(Ф/И)

Дано: ABCD - трапеция, МК - средняя линия. ВС = 13, МК = 25.

Найти: AD.

Решение задач по готовому чертежу (устно):

1. MN - средняя линия трапеции ABCD,

PR - средняя линия трапеции AMND.

ВС = 6 см, AD = 10 см.

Найти: MN и PR.

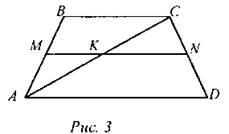
2. Чем являются отрезки МК и KN, если MN- средняя линия трапеции ABCD?

Решение:

Так как МК = (ВС + AD) : 2 = 25, то BC + AD = 50, AD = 50 - 13 = 37 см.

Ответ: 37 см.

1. MN = 8 см, PR = 9 см.

2. МК-средняя линия AABC, KN-средняя линия AACD

III этап. Работа в парах

Цель деятельности

Задания для самостоятельной работы

Создавать условия для формирования навыков решения задач

На каждом столе расположен листок с напечатанными задачами.

Задача 1.

Большее основание трапеции равно 8 см, а меньшее на 3 см меньше средней линии.

Найти: ВС, МК.

Дано:

ABCD - тоапеиия. AD = 8 см. МК - соедняя линия. ВС - ? на 3 см меньше МК.

Найти: ВС, МК.

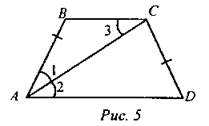
Решение:

Пусть ВС = x см, тогда МК = (х + 3) см

МК = (AD + ВС) : 2; х + 3 = (х + 8) : 2; 2х + 6 = х + 8; х = 2.

ВС = 2 см,

МК = 2 + 3 = 5 (см)

Ответ: ВС = 2 см, МК = 5 см.

Задача 2.

В равнобокой трапеции диагональ делит острый угол пополам. Периметр трапеции равен 54 дм, большее ее основание - 1,8 м. Вычислите меньшее основание трапеции.

Дано: ABCD - равнобокая трапеция. Р = 54 дм. AD = 1,8 м = 18 дм.

Найти: ВС.

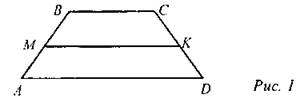
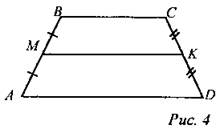
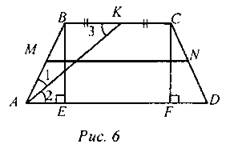
Решение:

∠1 = ∠2 так как АС - биссектриса ∠А; ∠2 = ∠3, как внутренние накрест лежащие углы.

∠1 = ∠2 и ∠2 = ∠3 => ∠1 = ∠3 => ∆АВС - равнобедренный.

Пусть АВ = ВС = CD = х.

Уравнение:

3х + 18 = 54

3х = 54 - 18

3х = 36

х = 12

Ответ: ВС = 12 дм.

Задача 3.

В равнобокой трапеции с острым углом 60° биссектриса этого угла делит меньшее основание, равное 16 см, пополам. Найдите среднюю линию трапеции.

Дано:

ABCD - равнобокая трапеция, ВС = 16 см.

АК - биссектриса ∠А

ВК = КС

МN - средняя линия

∠А = 60°

Найти: MN.

Решение:

Так как К - середина ВС, то ВК = КС = ВС : 2 = 16 см : 2 = 8 см.

Так как АК - биссектриса КА, то ∠1 = ∠2; ∠2 = ∠3 как внутренние накрест лежащие углы.

∠А = ∠D, АВ = CD, ∆AВЕ = ∆DCF (по гипотенузе и острому углу).

Значит, АЕ = DF, ∠АВЕ = 30°, ∆AВЕ - прямоугольный.

АЕ = АВ : 2; АЕ = 8 : 2 = 4 см.

DF = 4 см, EF = ВС = 16 см, AD = 16 + 4 + 4 = 24 см.

MN = (ВС + AD) : 2 = (16 + 24) : 2 = 20 см.

Ответ: MN = 20 см

IV этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Повторить свойства и признаки параллелограмма

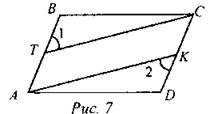
(И) 1. В параллелограмме один из углов в два раза меньше другого. Найти углы параллелограмма.

2. На рисунке ABCD - параллелограмм.

∠1 = ∠2. Докажите, что АТСК - параллелограмм.

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Составьте синквейн к уроку.

- Оцените свою работу на уроке

(И) Домашнее задание: № 379, 380