Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
График квадратичной функции - KBАДРАТИЧНАЯ ФУНКЦИЯ - САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - АЛГЕБРА
Вариант 1
1. Найдите координаты вершины параболы: у = -2x2 + 5x + 3.
2. Постройте график функции у = х2 + 3х - 4.
Найдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = -4;
в) нули функции;
г) промежутки возрастания и убывания функции.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:
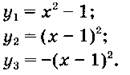
Вариант 2
1. Найдите координаты вершины параболы: у = 3х2 - 4х - 7.
2. Постройте график функции у = -х2 - 3х + 4.
Найдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = 4;
в) нули функции;
г) промежутки возрастания и убывания функции.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:
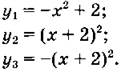
Вариант 3
1. Определите, при каких значениях b и с вершиной параболы у = х2 + bх + с является точка А(1; 3).
2. Постройте график функции у = (х - 2) (3х + 1).
Найдите:
а) ось симметрии параболы;
б) промежутки знакопостоянства функции;
в) область значений функции.
3. Опишите преобразования, с помощью которых из графика у = х2 можно получить график функции у = |3х2 - 12x + 9|.
Вариант 4
1. Определите, при каких значениях b и с вершиной параболы у = х2 + bх + с является точка А(3; -1).
2. Постройте график функции у = (2 - х)(2х + 3).
Найдите:
а) ось симметрии параболы;
б) промежутки знакопостоянства функции;
в) область значений функции.
3. Опишите преобразования, с помощью которых из графика у = х2 можно получить график функции: у = 3х2 - 6|x| + 6.