Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа) - KBАДРАТИЧНАЯ ФУНКЦИЯ - САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - АЛГЕБРА
Вариант 1
1. Функция задана формулой у = х2 + рх + q. Найдите р и q, если:
а) график функции пересекает оси координат в точках (0; 5) и (2; 0);
б) наименьшее значение, равное -3, функция достигает при х = 1.
2. Определите значение а, при котором график функции у = 3x2 + х + а лежит выше оси абсцисс.
3. Задайте формулой квадратичную функцию, график которой проходит через точки А(1; 3), B(-1; 9), С(3; 37).
4. Постройте график квадратичной функции у = х2 - 2х + а, если ее наименьшее значение равно 2.
5. Квадратичная функция задана формулой у = ах2 - (а + 3)x + 2.
Найдите а, если осью симметрии графика является прямая х = 1.
6. Определите значение р, при котором графики функции у = х2 – 4 и у = х2 + рх пересекаются в одной точке.
7. Постройте схематически график функции у = ах2 + bх + с, если известно, что а < 0, b > 0, с < 0, D > 0 (D — дискриминант квадратного трехчлена).
8. Найдите промежутки монотонности функций:
а) у = х2 - 3|х| + 2;
б) у = |х2 - 3х + 2|.
9. Постройте графики функций:
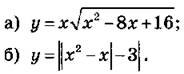
10. Дана функция f(x) = х2 + 2х. Постройте графики функций:

Вариант 2
1. Функция задана формулой у = х2 + рх + q. Найдите р и q, если:
а) график функции пересекает оси координат в точках (1; 10) и (0; 11);
б) наименьшее значение, равное 1, функция принимает при х = -3.
2. Определите значение а, при котором график функции у = -х2 + 5х + а лежит ниже оси абсцисс.
3. Задайте формулой квадратичную функцию, график которой проходит через точки А(-1; 3), В(1; 9), С(3; 55).
4. Постройте график квадратичной функции у = -х2 + 8x + а, если ее наибольшее значение равно 3.
5. Квадратичная функция задана формулой у = ах2 - (а + 3)x + 2. Найдите а, если осью симметрии графика является прямая х = -1/3.
6. Определите значение р, при котором графики функции у = х2 - р и у = х2 – 3x пересекаются в одной точке.
7. Постройте схематически график функции у = ах2 + bх + с, если известно, что а > 0, b < 0, с > 0, D < 0 (D — дискриминант квадратного трехчлена).
8. Найдите промежутки монотонности функций:
а) у = х2 - 7|х| + 10;
б) у = |x2 – 7x + 10|.
9. Постройте графики функций:
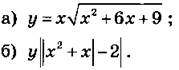
10. Дана функция f(x) = х2 - 4х. Постройте графики функций: