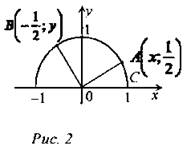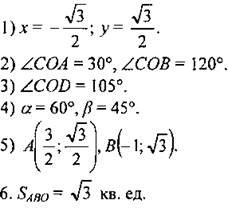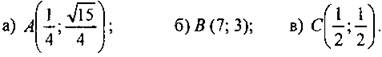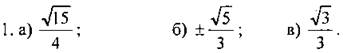Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СИНУС, КОСИНУС, ТАНГЕНС УГЛА - Урок 2 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
|
Цель деятельности учителя |
Совершенствовать навыки нахождения синуса, косинуса, тангенса для углов от 0° до 180°; способствовать развитию умения пользоваться основным тригонометрическим тождеством |
|||||
|
Термины и понятия |
Единичная окружность, синус, косинус, тангенс, котангенс, основное тригонометрическое тождество |
|||||
|
Планируемые результаты |
||||||
|
Предметные умения |
Универсальные учебные действия |
|||||
|
Умеют применить определения синуса, косинуса, тангенса и котангенса для определения координаты точки единичной окружности |
Познавательные: осознанно владеют логическими действиями определения понятий. Регулятивные: умеют осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группе, ясно, точно, грамотно излагать свои мысли. Личностные: проявляют познавательный интерес к изучению предмета |
|||||
|
Организация пространства |
||||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||||
|
Образовательные ресурсы |
Чертежи для задач |
|||||
|
I этап. Решение задач по готовым чертежам |
||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||
|
Совершенствовать навыки решения задач |
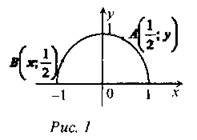
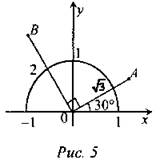
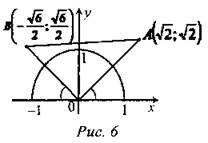
(Ф/И) 1. Решение задач по готовым чертежам. 1) Найти х и у:
2) Найти ∠СОА, ∠СОВ.
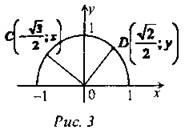
3) Найти ∠COD.
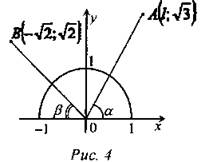
4) Найти α и β.
5) Найти координаты точек А и В; ОА = √3.
6) Найти SABO.
2. Проверка домашнего задания |
Ответы к задачам по готовым чертежам:
|
||||
|
II этап. Самостоятельная работа с взаимопроверкой |
||||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||||
|
Проверить уровень сформированности знаний по теме |
(И) Вариант I 1. Найдите: а) sinα, если cosα = -1/3; б) cosα, если sinα = 2/5; в) tgα, если cosα = 1/2. 2. Проверьте, лежат ли на единичной окружности точки:
3. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен α. Найдите координаты точки М, если: а) ОМ = 4; α = 60°; б) ОМ = 8; α = 150°. Ответы:
2. а) Да; б) нет; в) нет.
Вариант II 1. Найдите: а) sinα, если cosα = -1/4; б) cosα, если sinα = -2/3; в) tgα, если cosα = √3/2. 2. Проверьте, лежат ли на единичной окружности точки:
3. Угол между лучом ОP, пересекающим единичную полуокружность, и положительной полуосью Ох равен β. Найдите координаты точки P, если: а) ОP = 6; β = 30°; б) ОP = 10; β = 120°. Ответы:
2. а) Да; б) нет; в) нет.
|
|||||
|
III этап. Итоги урока. Рефлексия |
||||||
|
Деятельность учителя |
Деятельность учащихся |
|||||
|
(Ф/И) - Оцените свою работу на каждом этапе урока. - Какие трудности возникли при выполнении заданий и почему? ДЕРЕВО ЧУВСТВ Если чувствую себя хорошо, комфортно, то вешаю на дерево яблоки красного цвета, если нет, зеленого |
(И) Домашнее задание: решить задачи. 1. Постройте угол А, если cos∠A = -4/7. Найдите sin∠A, tg∠A. 2. Найдите значение выражения sin2а ∙ tga - cos2а, если известно, что sinα = 1/3. 3. Найдите наименьший угол между лучами ОА и ОВ, если А (-2; 2√3), В(5; 5), О - начало координат |
|||||