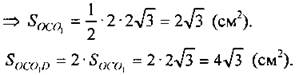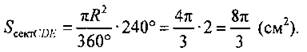РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА

Цель деятельности учителя

Создать условия для подготовки учащихся к контрольной работе

Термины и понятия

Круг, площадь круга, круговой сектор, площадь кругового сектора, длина окружности, длина дуги окружности

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют систематическими знаниями о плоских фигурах и их свойствах

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.

Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, контролировать процесс и результат учебной математической деятельности.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

* Тест

I этап. Тест с самопроверкой

Цель деятельности

Тестовые задания

Систематизировать теоретические знания по изученной теме

(И)

1. Один из внутренних углов правильного n-угольника равен 150°. Найдите число сторон многоугольника.

а) 9;

б) 14;

в) 12;

г) 15.

2. Периметр правильного треугольника равен 12√3 см. Найдите радиус вписанной окружности.

а) 2 см;

б) 4 см;

в) 4/√3 см;

г) 2/√3 см.

3. Около квадрата описана окружность, и в квадрат вписана окружность. Найдите отношение радиуса описанной окружности к радиусу вписанной окружности.

а) 1/√2;

б) √2;

в) 2;

г) 1/2.

4. Сторона правильного шестиугольника равна 2 м. На сколько площадь описанного круга больше площади вписанного круга?

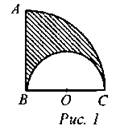
5. Площадь полуокружности с центром в точке О равна 8π. Найдите площадь заштрихованной фигуры.

а) 16π;

б) 8π;

в) 4π;

г) 32π.

6. В окружность вписаны квадрат и правильный треугольник. Периметр треугольника равен 30 см, периметр квадрата равен:

Ответы: 1 - в; 2 - а; 3 - б; 4 - г; 5 - б; 6 - а

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

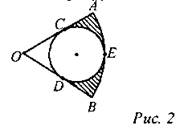
(Ф/И) Организует деятельность учащихся.

1. Даны стороны треугольника АВС - а, b, с и площадь S. Выразить радиусы описанной около треугольника и вписанной в него окружностей через а, b, с и S.

2. В сектор с центральным углом 60° и радиусом 6 см вписана окружность. Найти площадь заштрихованной фигуры.

1. Решение:

значит,

значит,

Ответ:

2. Решение:

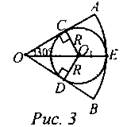
Так как окружность вписана в сектор, то ОА и ОВ - касательные к окружности, тогда OO₁ - биссектриса ∠COD, ОС ⊥ ОА. В ∆ОСО₁∠СОО₁ = 30°, СО₁ = R => ОО₁ = 2R.

тогда 3R = 2 см, ОО₁ = 4 см.

По теореме Пифагора

Найдем площадь кругового сектора, ограниченного дугой CDE:

Найдем площадь кругового сектора, ограниченного дугой АЕВ:

Ответ:

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Задайте три вопроса по уроку

(И) Домашнее задание: решить № 114, № 143