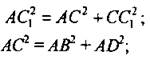ОБЪЕМ ТЕЛА. СВОЙСТВА ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ

Цели деятельности учителя

Создать условия для повторения понятия площади плоских фигур, введения понятий объема тела, единиц измерения объемов тел, для изучения основных свойств объемов и прямоугольного параллелепипеда, ознакомления учащихся с принципом Кавальери; способствовать развитию логического мышления учащихся

Термины и понятия

Призма, параллелепипед, грани, ребра, объем, принцип Кавальери

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют формулировать и обосновывать основное свойство диагоналей прямоугольного параллелепипеда, объяснять, что такое объем, и выводить формулу объема с помощью принципа Кавальери

Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации, устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и формулировать выводы.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Справочный материал по принципу Кавальери, чертежи для задач

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Систематизировать теоретические знания учащихся

(Ф/И)

1. Ответить на вопросы учащихся по домашнему заданию.

2. Проверить решение учащимися задач № 1190 (б) и № 1234 (б).

3. По готовому чертежу параллелепипеда на доске построить сечение параллелепипеда А плоскостью, проходящей через:

а) точки D, С и В₁.

б) точки В, К и L, где К - середина ребра АА₁ a L - середина СС₁.

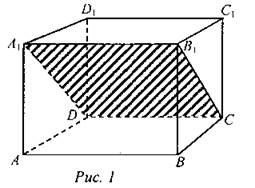
(Задача № 1235 в учебнике на с. 328.)

Решение:

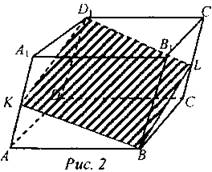
а) Проводим отрезок СВ₁, затем строим прямую DA₁ параллельную СВ₁. Параллелограмм CDA₁B₁ - искомое сечение (рис. 1).

б) По условию АК = КА₁ и C₁L = CL. Проводим отрезки КВ и BL. Проводим отрезок DL, параллельный отрезку КВ.

Соединяем отрезком точки К и D₁ принадлежащие одной плоскости ADD₁A₁. Параллелограмм KBLD₁ - искомое сечение (рис. 2)

II этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Ввести понятие объема и вывести формулу для вычисления объема прямоугольного параллелепипеда

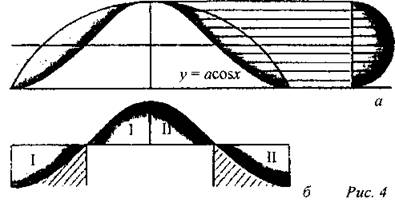
(Ф)

1. Повторить понятие площади плоской фигуры.

2. Ввести понятие объема тела по аналогии с понятием площади плоской фигуры. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром и обозначается так: 1 см³. Аналогично определяются кубический метр (м³), кубический миллиметр (мм³) и т. д.

3. Прочитать по учебнику текст (с. 306 и 308) и записать в тетрадях основные свойства объемов:

1) Равные тела имеют равные объемы.

2) Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 347): V = V_F + V_Q.

4. Разобрать по рисунку учебника (рис. 348) принцип Кавальери.

В XVII в. началась эпоха интегрального исчисления. Математики возвращались к задачам о вычислении площадей криволинейных фигур и объемов “кривых” тел, которыми так успешно занимался в древности Архимед. Интересовался этим вопросом и итальянский монах Бонавентура Кавальери (1598-1647). Он занимал кафедру математики в Болонском университете.

В переписке с астрономом и математиком Г. Галилеем они обсуждали разнообразные механические и математические проблемы, и в частности метод “неделимых”. Галилей собирался, но так и не написал книгу об этом методе. В 1635 г. вышла книга Кавальери “Геометрия, изложенная новым способом при помощи неделимых частей непрерывных величин”.

При вычислении площадей многоугольников бывает полезно преобразовывать фигуры, не меняя их площадей, например, разрезать на части и составлять новые. Так можно преобразовать друг в друга треугольники с равными основаниями и высотами. Можно ли аналогичным образом преобразовывать криволинейные фигуры? Кавальери представляет их себе состоящими из бесконечно тонких параллельных плоских слоев - “неделимых” или “нитей” (рис. 3) и утверждает, что площадь не меняется при сдвигах этих слоев друг относительно друга. Иначе, принцип Кавальери состоит в том, что если пересечь фигуру семейством всех прямых, параллельных заданной, то длины пересечений полностью определят площадь фигуры. В частности, если у двух фигур эти длины совпадают, то они равновелики. Строгого обоснования своего принципа Кавальери не дал, но рассмотрел его многочисленные применения. Например, на основе этого принципа легко выводится равновеликость треугольников с равными основаниями и высотами. Одно из самых удивительных применений принципа Кавальери принадлежит французскому математику Ж. Робервалю (1602-1675), который нашел площадь сегмента, ограниченного одной аркой циклоиды. В каждый момент времени Роберваль проектировал точку, двигающуюся по циклоиде, на вертикальный диаметр катящегося круга. Получалась новая кривая, которую Роберваль назвал спутницей циклоиды (рис. 4 а). Но потом выяснилось, что это синусоида, и это было первое (1634) появление ее в математике!

Площадь под аркой синусоиды легко вычисляется при помощи перехода к равносоставленному с ней прямоугольнику площадью 2п (рис. 4 б). Каждая из оставшихся двух фигур, которые называли лепестками Роберваля, по принципу Кавальери равновелика вертикальному полукругу, то есть общая площадь равна 3π.

Еще более эффективен принцип Кавальери при нахождении объемов тел. Он состоит в том, что объем тела определяется площадями его пересечений “всеми плоскостями”, параллельными некоторой заданной. Отсюда следует теорема о равновеликости пирамид с равновеликими основаниями и равными высотами, а эти пирамиды, как правило, не равносоставлены.

На этой теореме основывается формула для объема пирамиды. Очень удобен принцип Кавальери и для получения формул объемов круглых тел, скажем шара. Впишем в круговой цилиндр радиусом r и высотой 2r шар. Тело, являющееся дополнением шара до цилиндра, по принципу Кавальери равновелико телу, составленному из двух конусов, построенных на верхнем и нижнем основаниях цилиндра с вершиной в центре шара. Отсюда следует, что:

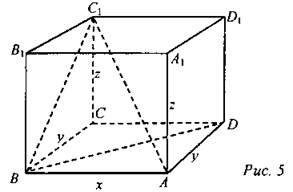
Интегральное исчисление содержит общие методы для вычисления площадей и объемов, причем там, где применение принципа Кавальери требовало нестандартных построений, к успеху приводят стандартные вычисления, и постепенно принцип Кавальери отошел в область истории. Однако, поскольку по принципу Кавальери легко вычисляются все “школьные” объемы и площади, неоднократно предлагалось принять принцип Кавальери в школьной геометрии за аксиому.

5. Когда мы говорим о размерах комнаты, имеющей форму прямоугольного параллелепипеда, то обычно употребляем слова “длина”, “ширина” и “высота”, имея в виду длины трех ребер с общей вершиной. В геометрии эти три величины объединяются общим названием: измерения прямоугольного параллелепипеда (рис. 349, с. 309).

6. У прямоугольника два измерения - длина и ширина. При этом, как мы знаем, квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (по теореме Пифагора для прямоугольника). Оказывается, что аналогичным свойством обладает и прямоугольный параллелепипед: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. (Используя рис. 349, провести доказательство этого свойства; рис. 349 заранее начертить на доске.) Доказательство записать на доске и в тетрадях:

следовательно,

7. Еще одно свойство прямоугольного параллелепипеда. Мы знаем, что площадь прямоугольника равна произведению его измерений. Аналогично объем прямоугольного па аллелепипеда равен произведению трех его измерений.

Для доказательства этого утверждения воспользуемся принципом Кавальери (прочитать доказательство по учебнику нас. 309-311, используя рис. 350).

8. В прямоугольном параллелепипеде с измерениями а, b, с, изображенном на рисунке учебника (рис. 350 б), площадь S основания равна ас, а высота h равна боковому ребру: h = b. Поэтому формулу V = а ∙ b ∙ с можно записать в виде V = S ∙ h, то есть объем прямоугольного параллелепипеда равен произведению площади основания на высоту

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

(Ф/И) Организует деятельность учащихся.

1. Решить задачу № 1193 (в).

2. Решить задачу № 1193 (б) (самостоятельно).

3. Решить задачу № 1194 на доске и в тетрадях.

4. Решить задачу № 1195.

5. Разобрать по учебнику решение задачи № 1198 (с. 315, используя рис. 357). Записать в тетрадях: “Объем призмы равен произведению площади основания на высоту”.

6. Решить задачу № 1197 (учитель объясняет решение задачи)

№ 1193 (в).

Решение:

Найти диагональ d.

(свойство диагонали прямоугольного параллелепипеда).

Ответ: 13.

№ 1197.

Решение:

AC₁ = 13 cm; BD = 12 см; BC₁ = 11 см. Обозначим измерения прямоугольного параллелепипеда х, у, z. Применим теорему Пифагора:

1) Для ∆ABD имеем х² + у² = 12² (1).

2) Для ∆BCC₁ имеем у² + z² = 11² (2).

3) По свойству диагонали прямоугольного параллелепипеда имеем x² + y² + z² = 13²(3).

4) Подставим в равенство (3) равенство (4), получим 12² + z² = 13², отсюда z² = 13² - 12², тогда z = 5; z = 5.

5) Подставим в равенство (2) значение z = 5, найдем у² + 5² = 11²;

6) Подставим значение у² = 96 в равенство (1), получим х² + 96 = 144;

7) Найдем объем:

Ответ: 240√2 см³

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Объясните, как измеряются объемы тел.

- Сформулируйте основные свойства объемов.

- Объясните, в чем заключается принцип Кавальери.

- Что такое измерения прямоугольного параллелепипеда?

- Сформулируйте свойство диагонали прямоугольного параллелепипеда.

- Чему равен объем прямоугольного параллелепипеда?

- Оцените свою работу на уроке

(И) Домашнее задание: изучить материал пунктов 126-127; сделать чертеж (рис. 357) и записать в тетрадях решение задач № 1193 (а), 1196, 1198