Свойства и графики элементарных функций - Числовые функции

Цель: обсудить свойства и графики некоторых функций.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Функция, возрастающая на промежутке.

2. Понятие нечетной функции и ее свойство.

3. Найдите область определения, область значений, монотонность и четность функции у = 3/x (с обоснованием). Постройте график функции.

Вариант 2

1. Функция, убывающая на промежутке.

2. Понятие четной функции и ее свойство.

3. Найдите область определения, область значений, монотонность и четность функции у = -2/x (с обоснованием). Постройте график функции.

III. Изучение нового материала

Теперь необходимо вспомнить основные свойства и графики некоторых ранее изученных функций (свойства надо представлять, но запоминать не стоит).

1. Линейная функция y = kх + m

1. Область определения - множество всех чисел D(f) = (-∞; +∞).

2. Графиком функции является прямая линия.

3. График функции пересекает ось абсцисс в точке х = -m/k (при k ≠ 0) и параллелен оси абсцисс при k = 0. График функции пересекает ось ординат в точке у = m.

4. Функция возрастает при k > 0, убывает при k < 0 и постоянна при k = 0.

5. Функция неограниченна при k ≠ 0 и ограничена при k = 0.

6. Функция определенной четности не имеет при m ≠ 0, нечетная при m = 0 и четная при k = 0.

7. Область значений - множество всех чисел при k ≠ 0 и у = m при k = 0.

8. При m = 0 функцию y = kх называют прямой пропорциональностью.

Пример 1

Найдем условие, при котором линейная функция у = kх + m является: а) нечетной; б) четной.

Область определения функции х ∈ (-∞; +∞) - симметричная. Найдем значение

а) Если функция нечетная, то у(-х) = -у(х). Получаем: -kх + m = -(kх + m), или m = -m, или 2m = 0, откуда m = 0.

б) Если функция четная, то y(-x) = y(x). Получаем: -kх + m = kх + m или 0 = 2kх, откуда k = 0 (так как х - любое число, не равное нулю).

2. Квадратичная функция y = kх² (k ≠ 0)

1. Область определения - множество всех чисел D(f) = (-∞; +∞).

2. Графиком функции является парабола.

3. График функции проходит через начало координат.

4. При k > 0 функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞). При k < 0 функция убывает на промежутке [0; +∞) и возрастает на промежутке (-∞; 0].

5. Функция ограничена снизу при k > 0 и сверху при k < 0.

6. Функция четная.

7. Область значений E(f) = [0; +∞) при k > 0 и E(f) = (-∞; 0] при k < 0.

8. Функция выпукла вниз k > 0 и вверх при k < 0.

Пример 2

Докажем ограниченность квадратичной функции у = х².

Очевидно, что при всех значениях х величина у =х² принимает только неотрицательные значения, т. е. у ≥ 0. По определению функция ограничена снизу, т. е. у > m (где т может быть любым отрицательным числом: m = -103, m = -5, m = -0,1).

3. Обратная пропорциональность у = k/x.

1. Область определения - множество всех чисел, кроме нуля.

2. Графиком функции является гипербола.

3. График функций осей координат не пересекает.

4. Функция возрастает при k < 0 и убывает при k > 0 в области определения.

5. Функция неограниченна.

6. Функция нечетна.

7. Область значений - множество всех чисел, кроме нуля.

8. При k > 0 функция выпукла вверх при х < 0 и вниз, при х > 0. При k < 0 функция выпукла вниз при х < 0 и вверх, при х > 0.

Пример 3

Выясним монотонность обратной пропорциональности у = k/x.

Область определения данной функции D(f) = (-∞; 0)U(0; +∞).

Рассмотрим два произвольных значения x₁ и х₂ (где х₂ > x₁) из области определения функции. Найдем значения функции в этих точках и сравним их. Для этого рассмотрим разность Так как х₂ > x₁, то разность x₁ - х₂ отрицательна. Поэтому знак разности f(х₂) - f(x₁) противоположен знаку дроби

Функция у = k/x не определена в точке х = 0. Рассмотрим два промежутка области определения. При x₁,х₂∈ (-∞; 0) и при x₁,х₂∈ (0; +∞) произведение x₁x₂ положительно. Поэтому знак разности f(x₂) – f(x₁) противоположен знаку коэффициента k. Следовательно, при k < 0 величина f(x₂) – f(x₁) > 0, т. е. f(x₂) > f(x₁) и функция возрастает; при k > 0 величина f(x₂) – f(x₁) < 0, т. е. f(x₂) < f(x₁) и функция убывает.

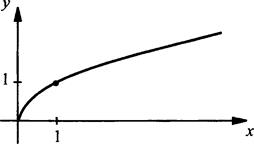
4. Функция у = у√х

1. Область определения - множество неотрицательных чисел D(f) = [0; +∞).

2. График специального названия не имеет.

3. График выходит из начала координат.

4. Функция возрастает.

5. Функция ограничена снизу, т. е. у ≥ 0.

6. Функция определенной четности не имеет.

7. Область значений - множество неотрицательных чисел.

8. Функция выпукла вверх.

5. Функция у = |x|

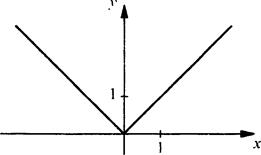
1. Область определения - множество всех чисел D(f) = (-∞; +∞).

2. График специального названия не имеет.

3. График проходит через начало координат.

4. Функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞).

5. Функция ограничена снизу, т. е. у ≥ 0.

6. Функция четная.

7. Область значений - множество неотрицательных чисел.

6. Квадратичная функция у = ax² + bх + с

1. Область определения - множество всех чисел D(f) = (-∞; +∞).

2. Графиком функции является парабола с вершиной в точке (х₀, у₀), где При а > 0 ветви параболы направлены вверх, при а < 0 - вниз. Прямая х = х₀ - ось симметрии параболы.

3. График функции пересекает ось ординат в точке у = С. При D = b² - 4ac > 0 график пересекает ось абсцисс в точках при D = 0 - график касается оси абсцисс в точке

4. При а > 0 функция убывает на луче (-∞; x₀] и возрастает на промежутке [x₀; +∞). При а < 0 функция убывает на луче [х₀; +∞) и возрастает на промежутке (-∞; х₀].

5. Функция ограничена снизу при а > 0 (т. е. у ≥ y₀) и сверху при а < 0 (т. е. у ≤ y₀).

6. Функция определенной четности не имеет.

7. Область значений E(f) = [у₀; +∞) при а > 0 и E(f) = (-∞; у₀] при а < 0.

8. Функция выпукла вниз при а > 0 и вверх - при а < 0.

Пример 4

На рисунке приведен график функции у = ах² + bх + с. Определим знаки коэффициентов а, b и с.

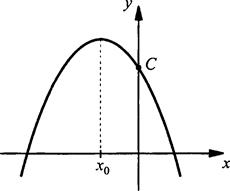
1) Так как ветви параболы направлены вниз, то коэффициент a < 0.

2) Абсцисса х₀ вершины параболы отрицательна (как видно из рисунка). Получаем неравенство: Умножим обе его части на отрицательное число 2а. При этом знак неравенства меняется на противоположный. Получаем: -b > 0. Вновь умножим обе части этого неравенства на отрицательное число -1. Опять знак неравенства меняется на противоположный. Имеем: b < 0. Значит, коэффициент b < 0.

3) При х = 0 значение функции y(х) равно у(0) = с. Из рисунка видно, что с > 0.

Итак, были определены знаки коэффициентов: а < 0, b < 0 и с > 0.

Пример 5

На рисунке приведен график функции у = ах² + bх + с. Определим знак выражения:

а) а + b + с; б) 4а – 2b + с.

Видно, что при всех значениях х функция у(х) принимает только положительные значения. Осталось понять смысл данных выражений. Найдем значение функции у = ах² + bх + с:

а) при x = 1 у(1) = a + b + c;

б) при x = -2 у(-2) = a ∙ (-2 )²+ b ∙ (-2) + c = 4a - 2b + с.

Напомним, что при всех значениях х (в том числе и при х = 1, и при х = -2) значения функции положительны. Поэтому a + b + с > 0 и 4а – 2b + с > 0.

Пример 6

График квадратичной функции у = ах² + bх + с проходит через точку А(-1; 10) и имеет вершину в точке B(1; -2). Напишем уравнение параболы.

Запишем условия прохождения параболы через точки А и В. Кроме того, учтем, что точка В - вершина параболы. Запишем выражение для абсциссы вершины. Получаем систему уравнений:

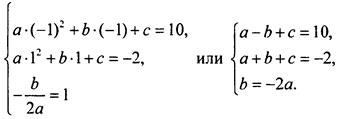
Вычтем из первого уравнения второе и получим -2b = 12, откуда b = -6. Тогда из третьего уравнения имеем -6 = -2а, откуда а = 3. Подставим значения а = 3 и b = -6 в первое уравнение и получим: 3 + 6 + с = 10, откуда с = 1.

Таким образом, напишем уравнение данной параболы у = 3х² - 6х + 1.

Пример 7

Найдем значение параметра к, при котором прямая у = 2x - 5 касается параболы у = х² + kx + 4. Найдем координаты точки касания.

Если графики двух функций пересекаются в точке с координатами (x₀; у₀), то величины х₀ и у₀ являются решением системы уравнений Если (x₀; у₀) - точка касания двух графиков, то приведенная система имеет единственное решение (x₀; у₀).

Приравняем правые части уравнений системы: х² + kх + 4 = 2х - 5 и получим квадратное уравнение с параметром х² + (k - 2)x + 9 = 0. Это уравнение (а следовательно, и приведенная система) имеет единственное решение, если дискриминант D = (k - 2)² – 4 ∙ 9 = k² – 4k -32 = 0. Корни этого уравнения k₁ = -4 и k₂ = 8.

а) При k = -4 уравнение х² + (k - 2)х + 9 = 0 имеет вид х² - 6х + 9 = 0 или (х - 3)² = 0. Корень этого уравнения х = 3, тогда у = 2х - 5 = 2 ∙ 3 - 5 = 1. Итак, при k = -4 данные парабола и прямая касаются в точке (3; 1).

б) При k = 8 уравнение х² + (k - 2)х + 9 = 0 имеет вид х² + 6х + 9 = 0 или (х + 3)² = 0. Корень этого уравнения х = -3, тогда у = 2х - 5= 2 ∙ (-3) - 5 = -11. Итак, при k = 8 данные парабола и прямая касаются в точке (-3; -11).

IV. Контрольные вопросы

1. Свойства и график линейной функции у = kх + m.

2. Свойства и график обратной пропорциональности у = k/x.

3. Свойства и график квадратичной функции у = kх².

4. Свойства и график функции у = √x.

5. Свойства и график функции у = |х|.

6. Свойства и график квадратичной функции у = ах² + bх + с.

V. Задание на уроках

§ 10, № 14; 16; 24 (а, г); 26; § 11, № 31 (а, б); 32 (в, г); 33 (а, б); 34 (в, г).

VI. Задание на дом

§ 10, № 15; 17; 24 (б, в); 27; § 11, № 31 (в, г); 32 (а, б); 33 (в, г); 34 (а, б).

VII. Творческие задания

1. Постройте график функции:

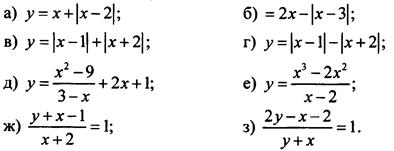
2. Постройте множество точек (х; у), координаты которых удовлетворяют условию:

3. Напишите уравнение параболы у = ах² + bх + с, которая проходит через точку А и имеет вершину в точке В:

Ответы: а) у = 2х² - 4х + 1; б) у = -х² + 6х - 5; в) у = 3х² + 6х - 7; г) у = -2х² - 8х + 3.

4. Найдите значение параметра k, при котором прямая y₁ касается параболы у₂. Найдите координаты точки касания.

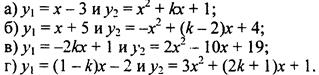
Ответы: а) при k = - 3 (2; -1), при k = 5 (-2; -5); б) при k = 1 (-1; 4), при k = 5 (1; 6); в) при k = -1 (3; 7), при k = 11 (-3; 67); г) при k = -2 (1; 1), при k = 2 (-1; -1).

5. Напишите уравнение параболы у = x² + px + q, если вершина ее находится в точке А:

а) A(1; -4); б) А(-1 - 5); в) А(2; -3); г) А(-4; -1).

Ответы: а) у = х² - 2х - 3; б) у = х² + 2х + 6; в) у = х² - 4х + 1; г) у = -х² - 8х - 17.

VIII. Подведение итогов уроков