Основные понятия и свойства неравенств - Рациональные неравенства и их системы

В этой главе будет рассмотрено решение основных видов алгебраических неравенств: линейных, квадратных и рациональных, а также их систем. Подобные неравенства возникают при исследовании функций, в текстовых задачах, в задачах на прогрессии и др.

Урок 1. Основные понятия и свойства неравенств

Цель: рассмотреть основные понятия, связанные с неравенствами.

Ход урока

I. Сообщение темы и цели урока

II. Изучение нового материала

Частично этот материал изучался в конце 8 класса. Теперь необходимо его упорядочить и систематизировать.

Рассмотрим неравенство f(х) v 0, где f(х) - функция, зависящая от переменной х, v - знак сравнения (может совпадать с одним из четырех знаков: >, <, ≥, ≤). Решением этого неравенства (или частным решением) называют такое значение переменной x, которое обращает неравенство f(x) v 0 в верное числовое неравенство. Множество всех частных решений неравенства называют общим решением (или решением) неравенства.

Пример 1

Числа 3; 1,6; √5; π - частные решения неравенства 2х - 3 ≥ 0 (в этом легко убедиться подстановкой таких решений в данное неравенство). Числа х, удовлетворяющие условию х ≥ 1,5, являются общим решением приведенного неравенства.

Применяются различные формы записи неравенств. В частности, используя перенос в другую часть неравенства его членов (с изменением их знаков на противоположные), мы имеем право записать общий вид неравенства в форме f(х) v g(x) (хотя, на наш взгляд, переход от одной формы записи неравенства к другой в учебнике не оправдан).

Два неравенства f(x) v g(x) и r(x) v s(x) называют равносильными, если они имеют одинаковые решения или решений не имеют. Можно дать и другое определение: два неравенства равносильны, если любое частное решение первого неравенства является частным решением второго и, наоборот, любое частное решение второго неравенства является частным решением первого.

Пример 2

а) Неравенства (2х² + 1)(2х - 3) ≥ 0 и 2х ≥ 3 равносильны, так как имеют одинаковые решения: х ≥ 1,5.

б) Неравенства 2х² + 1 < 0 и 3|х| + 2 < 0 равносильны, так как каждое из них не имеет решений.

в) Неравенства 2х - 3 ≥ 0 и (2х - 3)(4х - 20) ≤ 0 неравносильны, так как решение первого неравенства х ≥ 1,5, второго неравенства - 1,5 ≤ х ≤ 5. Таким образом, решения второго неравенства составляют только часть решений первого неравенства.

При решении неравенства его заменяют более простым равносильным неравенством. Такую замену называют равносильным преобразованием неравенства. Для этих преобразований используются три правила.

Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не меняя при этом знак неравенства.

Пример 3

Неравенство 3х + 4 < х² равносильно неравенству 0 < х² - 3х - 4, так как члены 3х и 4 перенесены в правую часть с противоположным знаком, а знак неравенства оставили неизменным.

Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не меняя при этом знак неравенства.

Пример 4

Неравенство 16х + 8 ≥ 20х² равносильно неравенству 4х + 2 ≥ 5х²: обе части неравенства разделили на положительное число 4, а знак неравенства сохранили.

Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Пример 5

Неравенство -3х² + 5х + 1 ≥ 0 равносильно неравенству 3х² - 5х - 1 ≤ 0, так как обе части первого неравенства умножили на отрицательное число (-1) и изменили знак неравенства на противоположный.

Правила 2 и 3 можно и нужно обобщить.

Правило 2*. Если обе части неравенства с переменной х умножить или разделить на одно и то же выражение р(х), положительное при всех значениях х, и сохранить знак неравенства, то получим неравенство, равносильное данному.

Пример 6

Неравенство равносильно неравенству 2х - 3 ≥ 0, так как обе части первого неравенства умножили на выражение положительное при всех значениях х, и сохранили знак неравенства.

Правило 3*. Если обе части неравенства с переменной х умножить или разделить на одно и то же выражение р(х), отрицательное при всех значениях х, и изменить знак неравенства на противоположный, то получим неравенство, равносильное данному.

Пример 7

Неравенство (-х⁴ - 1)(2х - 3) ≥ 0 равносильно неравенству 2х - 3 ≤ 0, так как обе части первого неравенства разделили на выражение р(х) = -х⁴ - 1 = -(х⁴ +1), отрицательное при всех значениях х, и изменили знак неравенства на противоположный.

Заметим, что формулировки правил 2* и 3* очень важны: только при соблюдении их условий получаются равносильные неравенства.

Пример 8

Неравенство разумеется, неравносильно неравенству 2х - 3 ≥ 0, так как выражение р(х) = х² - 1 в зависимости от х может иметь и положительный, и отрицательный знак. Поэтому просто умножить обе части данного неравенства на выражение р(х) = х² - 1 нельзя. Исходное неравенство равносильно двум системам неравенств Проще всего решить данное неравенство, разумеется, методом интервалов (который будет изложен позже).

III. Контрольные вопросы

1. Частное и общее решения неравенства.

2. Понятие равносильных неравенств.

3. Равносильные преобразования неравенств.

4. Три правила равносильных преобразований неравенств (фронтальный опрос).

IV. Задания на уроке и дома

1. Является ли данное число а решением неравенства?

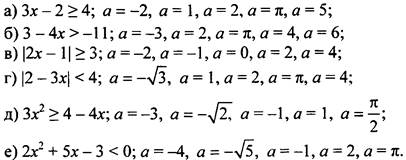
2. Являются ли данные неравенства равносильными и объясните почему:

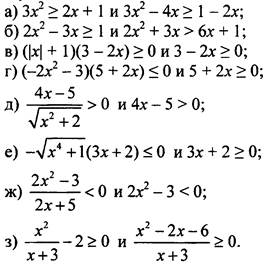
V. Подведение итогов урока