Линейные и квадратные неравенства - Рациональные неравенства и их системы

Цель: напомнить решение линейных и квадратных неравенств.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Второе правило равносильных преобразований неравенств.

2. Является ли данное число а решением неравенства?

2х² + х – 3 ≤ 0; а = -3, a = -1, a = 1, a = 2.

3. Являются ли данные неравенства равносильными и почему:

Вариант 2

1. Третье правило равносильных преобразований неравенств.

2. Является ли данное число а решением неравенства?

3х² - 5х - 2 ≥ 0; a = -2, a = 1, a = 2, a = 4.

3. Являются ли данные неравенства равносильными и почему:

III. Изучение нового материала

Неравенство f(x) v 0 называют по типу функции f(х). Линейным неравенством называют неравенство вида ax + b v 0, так как функция f(x) = ax + b линейная. Квадратным неравенством называют неравенство вида ax² + bx + с v 0, так как функция f(х) = ах² + bх + с квадратная (или квадратичная). Напомним решение линейных и квадратных неравенств, которое основано на результатах предыдущего урока. Сначала рассмотрим наиболее типичные линейные неравенства.

Пример 1

Решим неравенство

Чтобы избавиться от знаменателей дробей, умножим обе части неравенства на наименьшее общее кратное знаменателей дробей НОК (6, 3, 2) = 6. Так как число 6 положительное, то сохраним знак неравенства и по правилу 2 получим равносильное неравенство: или 2х - 7 + 2(7х - 2) ≤ 18 - 3(1 - х), или 2х - 7 + 14х - 4 ≤ 18 - 3 + 3х. В каждой части неравенства приведем подобные члены: 16х - 11 ≤ 15 + 3х. Перенесем члены, содержащие х, в левую часть неравенства, числа - в правую часть. При этом изменим знаки таких членов на противоположные и сохраним знак неравенства. По правилу 1 получаем равносильное неравенство 16х - 3х ≤ 15 + 11. В каждой части неравенства вновь приведем подобные члены: 13х ≤ 26. Чтобы найти решение неравенства, разделим обе его части на положительное число 13 и по правилу 2 получим х ≤ 2 или х ∈ (-∞; 2].

Часто встречаются двойные линейные неравенства.

Пример 2

Решим неравенство

Из всех частей неравенства вычтем число 3 и сохраним знаки неравенства. По правилу 1 (его можно трактовать и иначе: если из обеих частей неравенства вычесть один и тот же член и сохранить знак неравенства, то получим неравенство, равносильное данному) имеем равносильное неравенство: или Умножим все части неравенства на отрицательное число и изменим знаки неравенства на противоположные. По свойству 3 получим равносильное неравенство: или 1,5 > х ≥ -1,5, или х ∈ [-1,5; 1,5).

Также распространены неравенства, содержащие знаки модуля. Сначала напомним определение модуля. Модулем числа (выражения) а называют число (выражение) а, если а неотрицательно, и число (выражение) с противоположным знаком (-а), если а отрицательно, т. е. Геометрический смысл |а| - расстояние от точки а до точки 0 на координатной оси, т. е. |а| = р(а; 0) (см. рис.). Геометрический смысл |a - b| - расстояние между точками а и b на координатной оси, т. е. |а; b| = р(а; b).

Для решения простейших неравенств достаточно геометрического смысла модуля.

Пример 3

Решим неравенство |х - 3| ≤ 2.

Геометрический смысл данного неравенства: надо на координатной прямой найти такие точки х, для которых расстояние до точки 3 не больше 2. Посчитаем границы этого диапазона: 3 – 2 = 1 и 3 + 2 = 5. Тогда решение данного неравенства - интервал [1; 5].

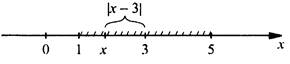
В более сложных случаях необходимо использовать определение модуля.

Пример 4

Решим неравенство |х| ≤ 2х + 3.

Используя определение модуля, надо рассмотреть два случая.

а) Если х ≥ 0, то данное неравенство имеет вид x ≤ 2х + 3. Его решение х ≥ -3 или интервал х ∈ [-3; +∞). Однако условию х ≥ 0 удовлетворяет только часть этого решения - промежуток х ∈[0; +∞), что и является решением данного неравенства в этом случае.

б) Если х < 0, то исходное неравенство имеет вид -х ≤ 2х + 3 или -3 ≤ 3x, откуда х ≥ -1. С учетом условия x < 0 получаем решение данного неравенства в этом случае - интервал х ∈ [-1; 0).

Учитывая результаты случаев а и б, найдем окончательное решение данного неравенства - промежуток х ∈ [-1; +∞).

Данное неравенство допускает простое и наглядное графическое решение. Построим графики функций у₁ = |х| и у₂ = 2х + 3.

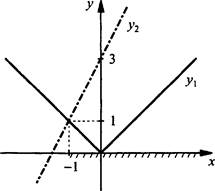
Смысл неравенства у₁ ≤ у₂: надо найти такие значения х, при которых график функции y₁ расположен не выше графика функции у₂. Эти графики пересекаются в точке (-1; 1). Видно, что неравенство выполняется при х ∈ [-1; +∞).

Другой разновидностью линейных неравенств являются неравенства с параметрами.

Пример 5

При всех значениях параметра р решим неравенство (р - 3)х ≥ р² - 9.

Другими словами, для каждого значения параметра р надо указать, при каких значениях х неравенство выполняется. Очевидно, что данное неравенство является линейным по переменной х. Чтобы найти х, надо обе части исходного неравенства разделить на коэффициент при х, т. е. на р - 3. Но эта величина может иметь разный знак. Поэтому по правилам 2 и 3 получим разный результат. Значит, надо рассмотреть три случая.

а) Если р - 3 < 0 (т. е. р < 3), то по правилу 3 получаем: или х ≤ р + 3, или x ∈ (-∞; р+3]. Заметим, что при этом знак неравенства изменился на противоположный.

б) Если р - 3 = 0 (т. е. р = 3), то, разумеется, делить обе части данного неравенства на выражение р - 3 нельзя. Поэтому подставим значение р = 3 в исходное неравенство. Получим неравенство 0 ∙ х ≥ 0, которое выполняется при всех значениях х. Поэтому решение неравенства в этом случае: х ∈ (-∞; +∞).

в) Если р - 3 > 0 (т. е. р > 3), то по правилу 2 получаем: или х ≥ р + 3, или х ∈ [р+3; +∞). Отметим, что при этом знак неравенства сохранился.

Обратим внимание на форму записи ответа. Ответ принято записывать в порядке возрастания параметра, и решение неравенств приводить в виде числовых промежутков. Итак, ответ: при р ∈ (-∞; 3) х ∈ (-∞; p+3], при p = 3 х ∈ (-∞; +∞), при р ∈ (3; +∞) х ∈ [р+3, +∞).

Теперь рассмотрим решение квадратных неравенств. Подобные неравенства удобно решать графически.

Решение сводится к нахождению промежутков х, в которых функция у = ах² + bх + с имеет положительные или отрицательные значения. Для этого надо определить, как расположен график функции у = ах² + bх + с в координатной плоскости: направление ветвей параболы (вверх или вниз) и точки пересечения ее с осью х (если они имеются). Рассмотрим соответствующие примеры.

Пример 6

Решим неравенство 6х² - х - 1 ≤ 0.

Рассмотрим функцию у = 6х² - х - 1. Ее графиком является парабола с ветвями, направленными вверх. Найдем точки пересечения параболы с осью абсцисс. Для этого решим уравнение 6х² - х - 1 = 0. Его корни х₁ = -1/3 и х₂ = 1/2.

Нарисуем график. Видно, что функция принимает неположительные значения на промежутке х ∈ [-1/3; 1/2]. Поэтому этот промежуток и является решением данного неравенства.

Пример 7

Решим неравенство

Рассмотрим функцию Ее графиком является парабола с ветвями, направленными вниз. Найдем точки пересечения параболы с осью абсцисс. Для этого решим уравнение Оно имеет единственный корень х = 3. Поэтому парабола касается оси абсцисс в точке х = 3.

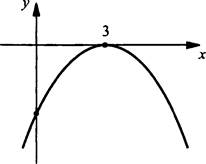
Нарисуем график. Видно, что функция принимает неотрицательные значения (а именно у = 0) только в единственной точке х = 3. Поэтому данное неравенство имеет решение х = 3.

Из рассмотренных примеров уже можно сформулировать алгоритм решения неравенства ax² + bx + c v 0.

1) Определяют направление ветвей параболы: при а > 0 - вверх, при а < 0 - вниз.

2) Находят дискриминант D = b² - 4ас квадратного трехчлена ах² + bх + с и определяют, имеет ли трехчлен корни.

3) Если трехчлен имеет корни, то отмечают их на оси абсцисс. С учетом направления ветвей строим эскиз параболы, проходящий через построенные на оси x точки.

4) Если трехчлен не имеет корней, строим эскиз параболы, расположенный в верхней полуплоскости при а > 0 и в нижней полуплоскости при а < 0.

5) Находят на оси х промежутки, для которых выполнено данное неравенство.

Разумеется, графический способ может быть использован и для решения более сложных неравенств.

Пример 8

Решим неравенство |х + 1|(х - 3) ≥ 0.

Рассмотрим функцию у = |х + 1|(х - 3) и построим ее график. Для этого раскроем знак модуля, рассмотрев два случая. При х ≥ -1 получаем функцию у = (х + 1)(х - 3). Ее графиком является парабола, направленная ветвями вверх и проходящая через точки х₁ = -1 и x₂ = 3. Из этой параболы сохраним участок ВС, для которого х ≥ -1.

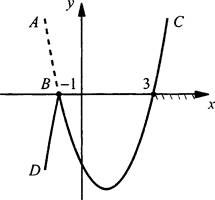
При х < -1 получаем функцию у = -(х + 1)(х - 3), которая отличается от предыдущей только знаком. Поэтому участок АВ (для х < -1) предыдущей параболы отражаем зеркально вниз и получаем часть BD требуемого графика. Таким образом, построен график данной функции.

Видно, что данное неравенство (у ≥ 0) выполняется для отдельной точки х = -1 ив промежутке [3; +∞). Поэтому решение неравенства x ∈ {-1}U[3; +∞).

Пример 9

Решим неравенство х² - (а + 4)х + 4а ≤ 0.

Найдем дискриминант квадратного трехчлена D = (а + 4)² – 4 ∙ 4а = а²+ 8a + 16 - 16a = (a - 4)²и его корни т. е. х₁ = а и х₂ = 4. Поэтому графиком квадратичной функции у = х² - (а + 4)х + 4а является парабола, направленная ветвями вверх и имеющая с осью абсцисс две или одну общие точки. Поэтому необходимо рассмотреть три случая.

а) Пусть x₁ < x₂, т. е. а < 4. Соответствующий график приведен на рисунке.

Видно, что значения функции у ≤ 0 на промежутке [а; 4]. Этот промежуток является решением неравенства в данном случае.

б) Пусть х₁ = х₂, т. е. a = 4. В этом случае парабола касается оси абсцисс в точке x = 4. Соответствующий график приведен на рисунке.

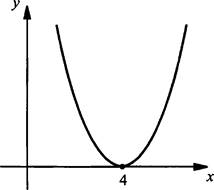
Видно, что значения функции или положительны или значение равно нулю. Последнее имеет место только в точке х = 4. Эта точка и является решением неравенства в этом случае.

В) Пусть x₁ > х₂, т. е. a > 4. График приведен на рисунке.

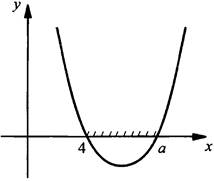
Видно, что значения функции у(х) неположительны на промежутке [4; а]. Этот промежуток является решением неравенства для данного случая.

Учитывая три рассмотренные ситуации, запишем окончательный ответ задачи: при а ∈ (-∞; 4) х ∈ [а; 4], при а = 4 х = 4, при а ∈ (4; +∞) х ∈ [4; а].

Рассмотрим наиболее удобный и универсальный способ решения любых неравенств - метод интервалов. Он с успехом может быть использован при решении всех типов неравенств, изучаемых в школе. Пока мы рассмотрим применение этого способа для целых и рациональных неравенств. Суть метода интервалов будет понятна из следующего примера.

Пример 10

Решим неравенство х² + 2х - 3 ≤ 0.

На числовой оси отметим корни уравнения х² + 2х - 3 = 0: х₁ = -3 и х₂ = 1. Эти точки разбили числовую ось на три промежутка: х ∈ (-∞; - 3); х ∈ [-3; 1] и х ∈ (1; +∞).

При х ∈ (-∞; -3) в многочлене х² + 2х - 3 = (х + 3)(x - 1) оба сомножителя отрицательны. Поэтому многочлен х² + 2х - 3 > 0 (отмечено знаком “+”) и неравенство не выполнено.

Для х ∈ [-3; 1] множитель (х + 3) становится неотрицательным, множитель (х - 1) по-прежнему отрицательный. Поэтому произведение (х + 3)(х - 1) < 0 (отмечено знаком “-”) и неравенство выполнено. Следовательно, интервал х ∈ [-3; 1] удовлетворяет неравенству.

При х ∈ (1; +∞) сомножители (х + 3) и (х - 1) положительны, произведение (х + 3)(х - 1) > 0 (отмечено знаком “+”) и неравенство не выполнено.

Заметим, что столь детальный анализ знаков при решении квадратных неравенств является излишним. Достаточно определить знак выражения х² + 2х - 3 в одной точке, не совпадающей с границами интервалов (например, при х = -10 выражение х² + 2х - 3 = (-10)² +2(-10) - 3 = 77 > 0). Кроме того, надо учесть, что при переходе к каждому следующему промежутку знак выражения х² + 2х - 3 меняется на противоположный. Поэтому диаграмма знаков, приведенная на рисунке, может быть получена сразу (решение неравенства отмечено штриховкой).

IV. Контрольные вопросы

1. Какое неравенство называется линейным?

2. Определение квадратного неравенства.

3. Модуль числа (выражения) и его геометрический смысл.

V. Задание на уроках

§ 1, № 2 (а); 3 (в, г); 4 (а); 7 (а, г); 10 (в, г); 14 (а, б); 17 (б); 19 (а, б); 21 (а); 22 (в, г); 24.

VI. Задание на дом

§ 1, № 2 (б); 3 (а, б); 4 (в); 7 (б, в); 10 (а, б); 14 (в, г); 17 (г); 19 (в, г); 21 (б); 22 (а, б); 25.

VII. Подведение итогов уроков