Числовые последовательности - Прогрессии

Цель: привести основные понятия, связанные с последовательностями.

Ход уроков

I. Сообщение темы и цели уроков

II. Изучение нового материала

1. Определение числовой последовательности

Множество чисел, для каждого из которых известен его порядковый номер, называют последовательностью.

Пример 1

а) В последовательности положительных нечетных чисел 1, 3, 5, 7, ... известно, что первое число равно 1, второе число равно 3, третье число равно 5 и т. д.

б) В последовательности правильных дробей с числителем 1 известно, что первое число равно 1/2, второе число равно 1/3, третье число равно 1/4 и т. д.

Числа, образующие последовательность, называют членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена: у₁, у₂, у₃, ..., у_n, ... . Соответственно, член последовательности с номером n (или n-й член последовательности) обозначают у_n, а саму последовательность - (у_n).

Пример 2

Рассмотрим последовательность натуральных трехзначных чисел: 100; 101; 102; ...; 999. В ней у₁ = 100, у₂ = 101, у₃ = 102, ..., у₉₀₀ = 999. Член этой последовательности с номером n (n-й член последовательности) можно вычислить по формуле у_n = 99 + n, где n = 1, 2, 3, ..., 900.

Последовательность может содержать бесконечно много членов (пример 1). Такую последовательность называют бесконечной. Последовательность может содержать и конечное число членов(пример 2). Такую последовательность называют конечной.

2. Способы задания последовательностей

Последовательность необходимо задать, т. е. указать способ, с помощью которого можно найти каждый ее член. Рассмотрим основные способы задания последовательностей.

1. Аналитический способ (формула n-го члена)

Последовательность задается формулой, которая позволяет найти по номеру n ее член у_n.

Пример 3

а) Пусть последовательность задана формулой у_n = 3n - 2. Подставляя вместо п натуральные числа, находим члены последовательности: и т. д. Имеем последовательность 1, 4, 7,....

б) Пусть последовательность задана формулой Подставляя вместо n натуральные числа, находим члены последовательности: и т. д. Имеем последовательность 0, 1, 0, 1, ... .

2. Аналитический способ (рекуррентная формула)

Последовательность задается формулой, которая позволяет найти следующие члены последовательности, если известны один или несколько предыдущих членов.

Пример 4

а) Пусть последовательность задана формулой где y₁ = 5 и n ≥ 1.

Запишем рекуррентную формулу для n = 1: или у₂ = 2 ∙ 5 + 3 = 13.

Пишем формулу для n = 2: или у₃ = 2 ∙ 13 + 3 = 29.

Запишем формулу для n = 3: или у₄ = 2 ∙ 29 + 3 = 61 и т. д.

Имеем последовательность 5, 13, 29, 61, ... .

б) Пусть последовательность задана формулой где у₁ = 1, у₂ = 2 и n ≥ 1.

Запишем рекуррентную формулу для n = 1: или или

Пишем формулу для n = 2: или

Запишем формулу для n = 3: или или и т. д.

Имеем последовательность 1, 2, 7, 20, 61, ... .

3. Описательный способ

Описывается способ получения членов последовательности.

Пример 5

а) Рассмотрим последовательность натуральных четных чисел. Из описания последовательности легко выписать ее члены: 2, 4, 6, 8, ... .

б) Рассмотрим последовательность приближений по недостатку с точностью до п цифр иррационального числа π. Из описания последовательности выписываем ее члены: 3; 3,1; 3,14; 3,141; 3, 1415;...

3. Основные свойства последовательностей

Теперь рассмотрим два основных свойства последовательностей.

1. Ограниченность последовательности

Последовательность (у_n) называют ограниченной, если существуют два таких числа m и М, что для любого натурального номера n выполнено неравенство m ≤ у_n ≤ М.

Пример 6

Докажем ограниченность последовательности

Найдем первый член последовательности и член последовательности с очень большим номером n, например Возникает гипотеза, что последовательность ограничена и m = 0 и М = 1. Поэтому надо доказать, что при всех натуральных значениях n выполнено неравенство Очевидно, что левая часть неравенства выполняется. Рассмотрим правую часть неравенства Так как выражение n + 2 положительно, то получаем неравенство n - 1 ≤ n + 2 или -1 ≤ 2, которое является верным.

2. Монотонность последовательности

Последовательность (у_n) называют возрастающей, если каждый ее член (начиная со второго) больше предыдущего, т. е. у_n+1 > у_n для n ≥ 1.

Последовательность (у_n) называют убывающей, если каждый ее член (начиная со второго) меньше предыдущего, т. е. у_n+1 < у_n для n ≥ 1.

Пример 7

Определим монотонность последовательности

Запишем (n + 1)-й член последовательности Найдем разность двух соседних членов Так как n - натуральное число, то при всех n дробь положительна. Поэтому у_n+1 – у_n > 0 или у_n+1 > у_n при всех n. Тогда по определению данная последовательность (у_n) возрастающая.

Как видно из этого урока, понятия последовательности и функции, их способы задания и свойства очень похожи. Поэтому последовательность (у_n) можно рассматривать как функцию у_nнатурального аргумента и, т. е. у_n = f(n). Тогда автоматически возникают понятия ограниченности и монотонности последовательности.

III. Контрольные вопросы

1. Дайте определение последовательности.

2. Основные способы задания последовательности.

3. Ограниченность последовательности.

4. Монотонность последовательности.

IV. Задание на уроках

§ 15, № 1; 6; 8; 10 (а); 12 (г); 16 (а); 18 (а, б); 19 (в, г); 20 (а, б); 23 (в, г); 35 (а, б); 37 (в, г); 39 (а, б); 41 (г).

V. Задание на дом

§ 15, № 2; 7; 9; 10 (б); 13 (б); 16 (г); 18 (г); 19 (а, б); 20 (в, г); 23 (а, б); 35 (в, г); 37 (а, б); 39 (в, г); 41 (б).

VI. Творческие задания

1. Найдите четыре первых члена последовательности (a_n), если:

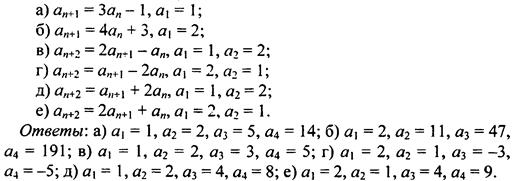
2. Докажите ограниченность последовательности (а_n):

3. Определите монотонность последовательности (а_n):

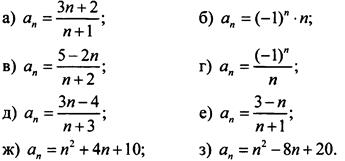
Ответы: а, д, ж) возрастающая; в, е) убывающая; б, г, з) немонотонная.

VII. Подведение итогов уроков