Поурочное планирование по алгебре 7 класс
Свойства действий над числами - I четверть - Выражения, тождества, уравнения
ЦЕЛЬ УРОКА: Актуализация, воспроизведение изучаемого материала и формирование у учащихся умений и навыков в его применении.
ПЛАН УРОКА:
№ |
Этап |
Содержание |
Время (мин) |
||
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
||
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
||
3 |
Устная работа |
Мотивация практической необходимости изучения свойств действий над числами |
7 |
||
4 |
Восприятие свойств действий над числами |
Повторить свойства действий над числами и показать использование этих свойств для рациональных вычислений |
6 |
||
5 |
Тренировочные упражнения |
Формировать умения применять свойства действий над числами для рационализации вычислений |
10 |
||
6 |
Самостоятельная работа |
Коррекция знаний |
8 |
||
7 |
Упражнения на повторение |
Повторить составление выражения но условию задачи, понятие двойного неравенства |
5 |
||
8 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
1 |
||
9 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
||
ХОД УРОКА
I. Организационный момент.
II. Проверка домашнего задания.
III. Мотивация практической необходимости изучения свойств действий над числами.
Устно:
1) Вычислить наиболее рациональным способом:
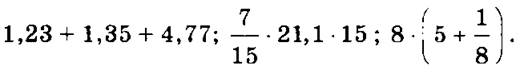
2) Прокомментировать, какие свойства действий над числами использованы.
IV. Восприятие свойств действий над числами
V. Самостоятельная работа (п.4 учебника).
1. Записать основные свойства для действий с переменными а и b; а, b и с в тетрадь.
2. Повторить формулировки свойств действий для любых чисел, приведенные на с. 230 учебника.
3. Решение примеров 1-4 записать в тетрадь.
VI. Тренировочные упражнения.
№ 70 (устно)
№№ 71 (а, в), 73 (а), 75 (а, б), 76 (а, б), 77 (а) — коллективно с записью на доске.
VI. Самостоятельная работа репродуктивного характера (с последующей проверкой).
№№ 71 (б, г), 73 (б), 75 (в, г), 76 (в, г), 77 (б).
VII. Упражнения на повторение.
№№ 80, 82.
VIII. Итог урока.
Повторить основные свойства сложения и умножения чисел.
IX. Домашнее задание.
п. 4,№ № 72 (а, в), 74 (а), 78 (а), 81.
Из истории математики
В эволюции алгебры различают 3 ступени: риторическую, синкопирующую и символическую.
Риторическая, или словесная, математика не пользуется символами. На этой ступени находились греческая математика до Диофанта (III в. н. э.), арабская и европейская математика до XIV века. Однако и там имеются особые знаки для некоторых математических понятий: у египтян иероглифы: скарабей — для понятия «равно», ноги, идущие против направления чтения — для понятия «больше», уходящие ноги — для понятия «меньше», неизвестное, искомое — иероглиф совы.
Синкопирующая математика употребляет для обозначения часто встречающихся понятий отдельные буквы или сокращения соответствующих слов. Например, для обозначения вычитания Диофант употреблял перевернутую букву Ф (пси), Лука Пачоли употреблял р и т для обозначения плюса и минуса.
Символическая математика начинается в XV веке. Введение в математику настоящей буквенной символики — заслуга француза Франсуа Виета (1540-1603).
Виет ввел буквенные обозначения для коэффициентов и неизвестного в уравнениях: например, он обозначает искомое — буквой N (Numerus), квадрат его — буквой Q (Quadratus), куб — буквой С (Cubus). Он пишет: NC-3N aeguatur 1, что означает: х3 – 3х = 1.
Англичанин Харриот (1631) заменяет большие буквы малыми. Наконец, Декарт (1596-1650) предлагает известные числа обозначать первыми а, 6, с, ..., неизвестные — последними х, у, z буквами латинского алфавита. Декарт в 1637 г. вводит для обозначения равенства особый знак =. В 1631 г. Харриот предлагает для обозначения неравенства теперешние значки > и <. В конце XV в. знаки « + » и «-» получают широкое распространение. Знак умножения ввел Аутрид (1631). Круглые скобки появились у Таргальи (1556), но лишь к середине XVIII в. скобки стали употребляться во всех математических книгах.
Современные знаки умножения в виде «·» и деления в виде «:» впервые использовал Лейбниц. Знак деления в 1684 г., а умножения — в 1698 г.