Что такое функция - I четверть - Функции

Данная тема является начальным этапом в обеспечении систематической функциональной подготовки учащихся. Здесь вводятся понятия «функция», «аргумент», «область определения функции», «график функции». Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции.

В данной теме начинается работа по формированию у учащихся умения находить по формуле значение функции по известному значению аргумента, выполнять то же задание по графику и решать обратную задачу по формуле и по графику.

Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида — прямой пропорциональной зависимости. Учащиеся должны понимать, как влияет знак коэффициента k на расположение в координатной плоскости графика функции у = kx, где k = 0, как зависит от значений k и b взаимное расположение графиков двух функций вида y = kx + b.

Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождается рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.

Обязательные результаты обучения

Теория

Понятие функции. Область определения функции. График функции. Линейная функция, ее график, геометрический смысл коэффициентов. Функция, описывающая прямую пропорциональную зависимость, ее график. Примеры графических зависимостей, отражающие реальные процессы.

Практика

Умение находить по формуле и по графику значение функции по известному значению аргумента и выполнять обратную задачу. Умение строить график линейной функции и прямой пропорциональности. Умение определять влияние знака коэффициента k на расположение в координатой плоскости графика функции у = kx, k = 0. Умение определять взаимное расположение графиков двух функций вида у = kx + b. Умение определять принадлежность точки графику.

---

1 В задачах под номером 4 ученик должен рассмотреть два случая: слова «одном» и «другом» не означают «первый» и «второй».

Урок 24

ТЕМА: Что такое функция

ЦЕЛЬ УРОКА: Формирование у учащихся понятия функции, способов ее задания, умения находить соответствующие значения функции.

ПЛАН УРОКА:

№	Этап урока		Содержание	Время (мин)
1	Организационный момент		Нацелить учащихся на урок	1
2	Анализ контрольной работы		Коррекция ошибок	8
3	Устная работа		Актуализация опорных знаний	5
4	Изучение нового материала		Ввести понятие функции, способов ее задания	9
5	Тренировочные упражнения		Формировать понятие функции, способов ее задания, умение находить соответствующие значения функции	12
6	Упражнение на повторение	Повторить решение текстовых задач с помощью уравнений		7
7	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке		1
8	Сообщение домашнего задания	Разъяснить содержание домашнего задания		2

ХОД УРОКА

I. Организационный момент.

II. Анализ контрольной работы.

III. Актуализация опорных знаний.

Устно:

1) Найти значение выражения 10x + 4, которое соответствует значению x, равному 6,7; -3,4; 1/5; 1/2; 0.

2) Выразить формулой зависимость между путем S, скоростью v и временем t при равномерном движении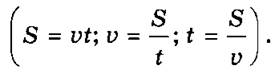

3) Выразить формулой зависимость между собственной скоростью парохода v1, скоростью течения v2 и скоростью парохода:

а) по течению v3;

б) против течения v4.

4) Какой формулой выражается зависимость между делимым а, делителем b, частным q и остатком r? (а = b · q + r).

5) Среди точек найти пары точек, симметричных относительно оси X, оси У, начала координат:

А(0; 5);

В(4,8; 3);

С(0; 2);

D(0,5; 2);

E(4,8; -3);

F(0; -2);

М(-4,8; 3).

IV. Изучение нового материала.

Фронтальная работа с классом (п. 12 учебника).

1. Ввести понятия: независимой переменной, зависимой переменной или функции, функциональной зависимости.

2. Познакомить учащихся со способами задания функций:

1) формулой (пример 1, пример 2 п. 12);

2) графиком (пример 3);

3) таблицей (пример 4).

3. Ввести понятия аргумента, области определения функции.

V. Тренировочные упражнения.

№ 258 — с записью в тетрадях и на доске. Образец оформления — примеры 1-4 п. 12;

№ 259 — самостоятельно с последующей проверкой;

№ 261 — устно;

№ 263 — в тетрадях и у доски.

VI. Упражнения на повторение.

№№ 265, 280 — самостоятельно с последующей проверкой.

VII. Итог урока.

Что называется функцией? Какие способы задания функции вы знаете?

VIII. Домашнее задание.

п. 12, №№ 260, 262, 264, 266.

Понятие функции — важнейшее понятие школьного курса математики. Это основной стержень, вокруг которого группируется все преподавание математики. «Потому, во-первых, что ни одно из других понятий не отражает явлений реальной действительности с такой непосредственностью и с: такой конкретностью, как понятие функциональной зависимости, в котором воплощены и подвижность, динамичность реального мира, и взаимная обусловленность реальных величин. Потому, во- вторых, что это понятие, как ни одно другое, воплощает в себе диалектические черты современного математического мышления; именно оно приучает мыслить величины в их живой изменчивости, а не в искусственно препарированной неподвижности, в их взаимной связи и обусловленности, а не в искусственном отрыве друг от друга. Потому, наконец, что понятие функциональной зависимости есть основное понятие всей высшей математики и что качество подготовки оканчивающих среднюю школу к усвоению курса математики в высшей школе в значительной степени измеряется тем, насколько твердо, полно и культурно они свыклись с этим важнейшим понятием» (А. Я. Хинчин (1894-1959), крупнейший советский математик, соратник Н. Н. Лузина, А.Н. Колмогорова).

Первоначально понятие функции как аналитического выражения сложилось в первой половине XVII в. В XVIII в. основным объектом изучения математики стали зависимости между переменными величинами. Термин «функция» (от латинского functio — совершение, выполнение) ввел И. Бернулли в 1718 г. Л. Эйлер предложил в 1748 г. определение функции как аналитического выражения.

В общем виде определение функции было дано Н. И. Лобачевским в 1834 г. В современной формулировке оно выглядит так: «Если каждому допустимому значению переменной величины х соответствует определенное значение переменной величины у, то х называется независимой переменной, а у — функцией от х».

В этой формулировке слово «соответствует» не говорит о способе задания зависимости переменных величин. Она может быть задана описанием, таблицей, аналитически, графически.

Соответственно к понятию функции можно подвести:

1) Рассматривая однозначные аналитические выражения зависимостей (Р = 4а — зависимость периметра квадрата от его стороны; С = 2r — зависимость длины окружности от ее радиуса, S = r2 — зависимость площади круга от его радиуса и т.д.), можно дать определение независимой переменной и функции.

При таком введении функции у учеников может возникнуть представление, что функция — аналитическое выражение. Поэтому важно также рассматривать зависимости, заданные не аналитически. Например, таблично, графически:

2) Рассматривая таблицы с парами значений: время суток и температура воздуха; длина стального стержня и его температура; высота столба масла и его давление на 1 см2 площади и др. необходимо сформировать у учащихся понятия независимой переменной и функции.

3) Многие приборы записывают непрерывно показания графически: термографы, барографы, сейсмографы, кардиографы и др. Работа с графиком позволяет дать определение независимой переменной и функции.

В каждом примере обязательно подчеркиваем, что каждому значению независимой переменной соответствует единственное значение зависимой переменной (т.е. функции).

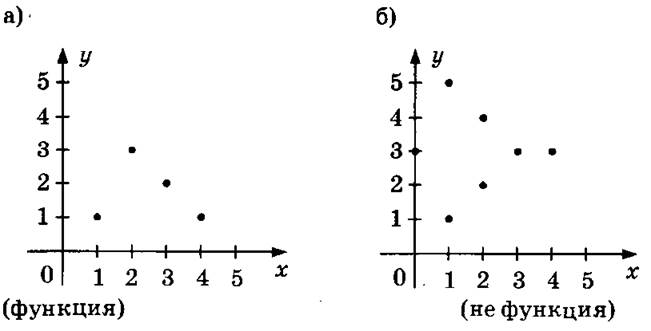
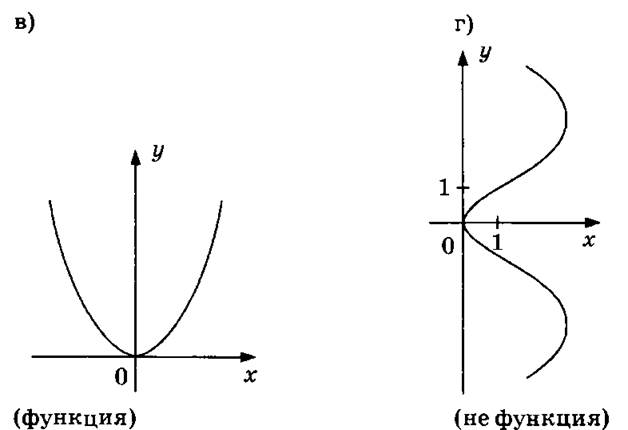
Полезно в связи с этим дать такое упражнение: можно ли зависимость переменной у от переменной х, представленную на рисунках а) - г), считать функцией?