Иррациональные числа - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ

Цель: дать понятие об иррациональных числах и множестве действительных чисел.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Какие числа относятся к рациональным?

2. Запишите десятичную дробь в виде обыкновенной: а) 2,75; б) 0,(7); в) 0,(73).

3. Представьте в виде десятичной дроби число: а) 1/80; б) 5/17.

4. Найдите |3 · 2,8 - 11,6|.

Вариант 2

1. В каком виде записываются рациональные числа?

2. Запишите десятичную дробь в виде обыкновенной: а) 1,25; б) 0,(4); в) 0,(37).

3. Представьте в виде десятичной дроби число: а) 1/40; б) 3/13.

4. Найдите |2 · 3,7 - 10,9|.

III. Изучение нового материала (основные понятия)

Разумеется, кроме рациональных чисел существуют и другие числа.

Пример 1

Рассмотрим десятичную бесконечную дробь 0,10110111.... В этом числе после запятой выписана цифра 1, потом 0, затем 11, потом 0, далее 111, потом 0 и т. д.

Эта дробь является бесконечной и непериодической, т. к. количество единиц все время увеличивается. Поэтому в этой дроби нет повторяющихся групп цифр. Следовательно, такое число (по определению) не может быть рациональным. Подобные числа называют иррациональными (приставка «ир» означает «не»).

Таким образом, иррациональное число — десятичная бесконечная непериодическая дробь. Иррациональное число нельзя представить в виде отношения m/n и обратно: любое число, не представимое в виде m/n, является иррациональным.

Пример 2

Докажем, что сторона а квадрата с площадью 3 является иррациональным числом.

Докажем от противного. Предположим, что число a — рациональное, т. е. его можно представить в виде несократимой дроби (у которой числитель и знаменатель взаимно простые числа—по основному свойству дробей это всегда можно сделать, разделив числитель и знаменатель на их НОД). Тогда число a можно записать в виде a = m/n (n ≠ 1). Площадь квадрата со стороной а есть — несократимая дробь и не является натуральным числом (т. к. n2 ≠ 1 — натуральное число). С другой стороны, а2 = 3 — натуральное число. Поэтому получаем противоречие: одно и то же число а2 не может быть и несократимой дробью, и целым числом. Это противоречие свидетельствует о том, что число а не может быть рациональным, т. е. является числом иррациональным. Число а, которое является корнем уравнения а2 = 3, обозначают символом . Таким образом, было доказано, что — иррациональное число.

Иррациональные числа внешне могут иметь различный вид: (≈ 3,1416... — отношение длины окружности к ее диаметру) и т. д.

Рациональные и иррациональные числа называют действительными числами. Множество действительных чисел обозначают буквой R.

Например, На диаграмме представлена структура множества действительных чисел.

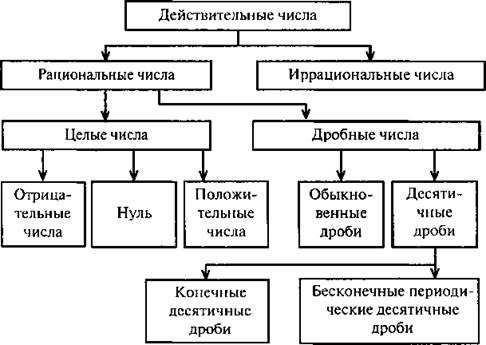
В математике приняты обозначения наиболее часто рассматриваемых множеств чисел:

множество натуральных чисел — N.

множество целых чисел — Z.

множество рациональных чисел – Q.

множество действительных чисел — R.

Изображение действительных чисел на числовой прямой Числовой осью называется прямая, на которой выбраны начало отсчета (точка нуль), положительное направление и масштаб.

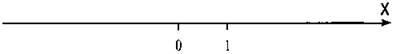
Тогда каждому действительному числу на оси 0x отвечает определенная точка. При этом положительные числа откладывают справа от точки О, отрицательные числа — слева. Также справедливо и обратное утверждение: любой точке на оси ОХ отвечает определенное число.

Пример 3

Отложить на числовой оси числа: а) -3; б) -2/3; в)

а) Возьмем числовую ось. С помощью циркуля раствором, равным единичному отрезку, слева отточки О отложим точку А. Очевидно, этой точке отвечает число (-1). Затем, не меняя раствора циркуля, от точки А влево откладываем точку В, которой отвечает число (-2). И наконец так же строим точку С, которой соответствует число (-3).

б) Воспользуемся теоремой Фалеса. Построим произвольный угол KON.

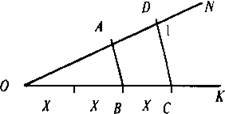
На стороне ON отложим с помощью циркуля отрезок OD, равный единичному отрезку. На стороне ОК отложим три произвольных равных отрезка длиной X. Тогда Теперь соединим точки С и D и построим отрезок AB||CD. Тогда по теореме Фалеса: Учтем, что OD = 1 и получим ОА = 2/3. Затем возьмем числовую ось и с помощью циркуля перенесем отрезок ОА влево от начала отсчета.

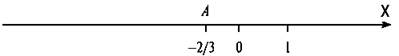
в) Воспользуемся теоремой Пифагора. Построим прямой угол KON и на его сторонах отметим единичные отрезки ОА и ОВ.

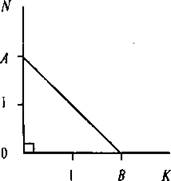
Тогда по теореме Пифагора длина отрезка АВ равна:

Теперь возьмем числовую ось и с помощью циркуля перенесем отрезок АВ, отложив его справа от начала отсчета.

Из рассмотренного примера видно, что только с помощью циркуля и линейки без делений можно строить на числовой оси целые, рациональные и иррациональные числа.

Из двух действительных чисел больше то число, которое располагается правее на числовой прямой. При этом бесконечные десятичные дроби сравнивают по тем же правилам, что и конечные десятичные дроби.

Пример 4

а) Сравним числа 3,176... и 3,169.... В этих положительных бесконечных десятичных дробях совпадают целые части и цифры десятых. Но в разряде сотых у первой дроби число единиц больше, чем у второй. Поэтому первая дробь больше второй, т. е. 3,176... > 3,169... (см. рис.).

Следовательно, на числовой прямой первое число располагается правее второго.

б) Сравним числа 0,16 и 1/6. Дробь 1/6 запишем в виде бесконечной десятичной дроби 1/6 = 0,1(б) и сравним десятичные дроби 0,16 и 0,1(6). У этих дробей совпадают целые части и цифры десятых и сотых. Однако у второй дроби цифра тысячных больше. Поэтому вторая дробь больше первой, т. е. 0,16 < 0,1(6) или 0,16 < 1/6.

в) Сравним числа 3,148... и -2,124... . Первое из этих чисел положительное, второе — отрицательное. Поэтому первое число больше, т. е. 3,148... > -2,124...

Действительные числа можно складывать, вычитать, умножать и делить (если делитель не равен нулю). Действия с действительными числами обладают теми же свойствами, что и действия с рациональными числами. При выполнении действий с действительными числами их заменяют приближенными значениями. Повышая точность приближенных значений, получают более точное значение результата.

Пример 5

Найдем приближенное значение суммы чисел а = 1/3 и b = 2,1437... .

Запишем число а в виде десятичной дроби а = 0,(3). Возьмем приближенные значения слагаемых с точностью до 0,1: а ≈ 0,3 и b ≈ 2,1. Тогда сумма а + b ≈ 0,3 + 2,1 = 2,4. Если взять более точные приближенные значения слагаемых с точностью до 0,01 (т. е. а ≈ 0,33 и b ≈ 2,14), то получим более точное значение суммы: а + b = 0,33 + 2,14 = 2,47.

Пример 6

Найдем длину окружности и площадь круга радиуса R = 3 м.

Возьмем приближенное значение π ≈ 3,14. Длина окружности l находится по формуле l = 2πR. Поэтому получаем l ≈ 2 · 3,14 · 3 = 18,84 (м). Площадь круга S находится по формуле S = πR2. Поэтому имеем S = 3,14 · 32 = 28,26 (м2).

IV. Контрольные вопросы

1. Какие числа называются иррациональными? Приведите примеры.

2. Какие числа образуют множество действительных чисел? Как обозначают множество действительных чисел?

3. Структура действительных чисел (диаграмма).

4. Какие действительные числа можно и какие нельзя представить в виде отношения m/n (где m — целое число, n — натуральное число)?

5. Изображение действительных чисел на числовой прямой.

6. Сравнение действительных чисел.

V. Задание на уроке

№ 270; 273 (б); 274 (а, в); 275 (б, в, д); 276 (а, б); 277; 279; 281.

VI. Задание на дом

№ 271; 272; 273 (а); 274 (б, г); 275 (а, г, е); 276 (в, г); 278; 280; 282.

VII. Подведение итогов урока