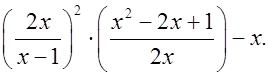Поурочные разработки по Алгебре 8 класс
ПОВТОРЕНИЕ: АЛГЕБРАИЧЕСКИЕ ДРОБИ
Цели: провести анализ контрольной работы; повторить правила выполнения действий с алгебраическими дробями; рассмотреть различные примеры на упрощение выражений различной сложности.
Ход урока
I. Организационный момент.
II. Анализ контрольной работы.
Выставить оценки за контрольную работу.
В а р и а н т 1
Задание 5*.
Найдите область определения данной функции: 
Р е ш е н и е:
Чтобы найти область определения данной функции, надо определить при каких значениях x дробь  имеет смысл. Необходимо, чтобы подкоренное выражение было неотрицательным и в знаменателе не было 0.
имеет смысл. Необходимо, чтобы подкоренное выражение было неотрицательным и в знаменателе не было 0.
x2 + 3x – 10 ≥ 0;
x2 + 3x – 10 = 0;
x1 = –5, x2 = 2;
x ![]() (–∞; –5]
(–∞; –5]![]() [2; +∞).
[2; +∞).
x + 5 ≠ 0, x ≠ –5.
Область определения данной функции: (–∞; –5)![]() [2; +∞).
[2; +∞).
В а р и а н т 2
Задание 5*.
Найдите область определения данной функции: 
Р е ш е н и е:
Для дроби 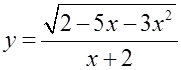 необходимы условия:
необходимы условия:
2 – 5x – 3x2 ≥ 0
x + 2 ≠ 0
3x2 + 5x – 2 ≤ 0;
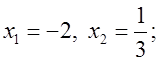
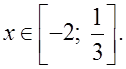
x + 2 ≠ 0, x ≠ –2.
Область определения данной функции 
III. Решение задач.
1) Повторить на примере элементарных примеров правила выполнения действий с алгебраическими дробями:
а) 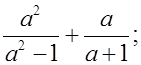 б)
б) 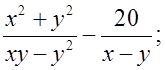
в)  г)
г) 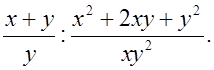
2) Рассмотреть простые выражения на все действия с алгебраическими дробями:
а)  б)
б) 
в)  г)
г) 
3) Рассмотреть более сложные выражения на упрощение:
а) 
б) 
в) 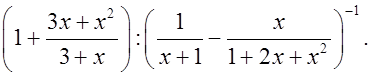
4) Повторить правила упрощения выражений с отрицательными целыми степенями. Рассмотреть упрощение выражений на данную тему (подставить и вычислить в заданных примерах):
а) 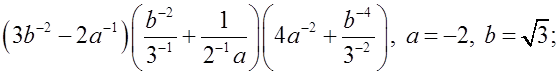
б) 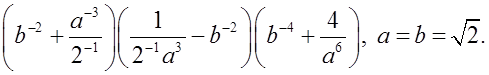
IV. Подведение итогов.
Домашнее задание: упростить