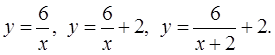Поурочные разработки по Алгебре 8 класс
Урок 2 - КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = f(x + l) + m, ЕСЛИ ИЗВЕСТЕН ГРАФИК ФУНКЦИИ y = f(x)
Цели: закрепить умение строить график функции y = f(x + l) + m, если известен график функции y = f(x); повторить правило выделения квадрата двучлена; развивать у учащихся умение строить графики различных функций и решать уравнения графическим способом; проверить умение строить графики различных функций с помощью шаблонов.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
Четыре ученика выходят к доске для построения графиков функций, заданных на карточках:
Карточка 1 y = x2, y = x2 + 3, y = (x – 1)2 + 3. |
Карточка 2
|
Карточка 3 y = –2x2, y = –2(x + 3)2, |
Карточка 4
|
III. Актуализация знаний.
1) Пока на доске проходит индивидуальная работа, остальные учащиеся класса, проверив домашнее задание, работают по карточкам.
Известно, что используются только две функции y = x2 и 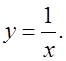 По данным на карточках графикам нужно назвать функции (карточки готовятся на отдельных листах).
По данным на карточках графикам нужно назвать функции (карточки готовятся на отдельных листах).
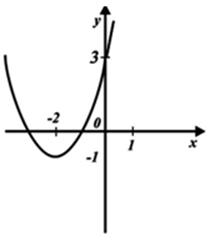
О т в е т: y = (x + 2)2 – 1.
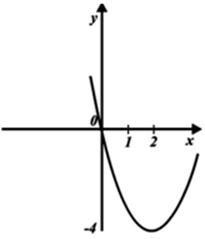
О т в е т: y = (x + 2)2 – 4.
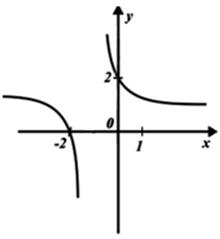
О т в е т: 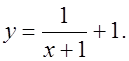
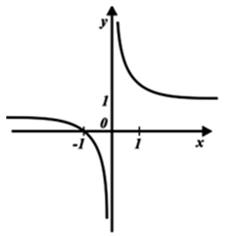
О т в е т: 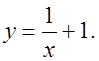
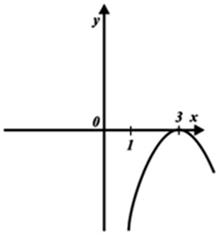
О т в е т: y = –(x –3)2.
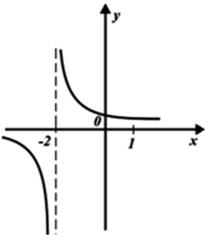
О т в е т: 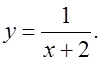
2) Решаются задания № 21.12; 21.13; 21.24.
3) Повторить формулы сокращенного умножения, выписать на доску формулы квадрата суммы и разности.
Заменить звездочки числами таким образом, чтобы равенства стали верными:
а) ![]() в)
в) ![]()
в) ![]() г)
г) ![]()
4) Выделить полный квадрат из трехчлена:
а) x2 – 8x + 14 = (x2 – 2 ⋅ 4 ⋅ x + 16) – 16 + 14 = (x – 4)2 – 2.
б) z2 + 6x + 10 = (x2 – 2 – 3 ⋅ x + 9) – 9 + 10 = (x + 3)2 + 1.
IV. Объяснение нового материала.
Задания для учащихся:
Построить график функции у = x2 – 6x + 8.
Один ученик на доске выполняет преобразования по выделению полного квадрата: y = (x2 – 2 ⋅ 3 ⋅ x + 9) – 9 + 8 = (x – 3)2 – 1
Другой ученик строит график функции y = (x – 3)2 – 1.
(Можно использовать любой алгоритм: сдвиг или вспомогательную систему координат.)
Делается вывод:
Для построения графика функции y = ax2 + bx + c нужно сначала преобразовать функцию, то есть выделить полный квадрат, а затем построить график.
V. Закрепление нового материала.
Разобрать решение заданий № 21.27, в классах с высоким уровнем подготовки № 21.28 (а, г).
VI. Самостоятельная работа.
Вариант 1 |
Вариант 2 |
На координатной плоскости с помощью шаблонов построить графики данных функций |
|
1) y = 2x2 – 1; 2) 3) 4) y = x2 – 2x – 1. |
1) 2) y = 0,5(x + 2)2; 3) y = –(x – 3)2 + 6; 4) y = x2 + 2x + 2. |
VII. Подведение итогов.
Домашнее задание: выполнить задания № 21.15; 21.23; 21.26.