Урок 1 - СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

Цели: провести анализ контрольной работы; ввести свойства неравенства; формировать умение сравнивать числа и выражения, а так же умение пользоваться свойствами неравенств.

Ход урока

I. Организационный момент.

II. Анализ контрольной работы.

Рассмотреть решение заданий, с которыми не справилось большинство учащихся, на доске.

III. Объяснение нового материала.

Учащиеся вспоминают правила сравнения натуральных чисел, десятичных дробей и обыкновенных дробей.

Устно сравнить:

126 и 97; 12,6 и 12,61; 1,876 и 2,876; 4,1 и 4,099;

и и и и

Далее учитель формулирует свойства числовых неравенств, свойства выписываются на доску и в тетради.

1) Если a > b и b > c, то a > c.

2) Если a > b, то a + c > b + c.

3) Если a > b и m > 0, то am > bm; если a > b и m < 0, то am < bm.

4) Если a > b и c > d, то a + c > b + d.

5) Если a, b, c, d – положительные числа и a > b, c > d, то ac > bd.

6) Если a и b – неотрицательные числа и a > b, то an > bn, где n – любое натуральное число.

В классах с высоким уровнем подготовки данные свойства доказываются.

IV. Закрепление нового материала.

1) Выполняется № 31.2; 31.4; 31.6; 31.7.

2) Свойства неравенств закрепляются на примерах № 31.12; 31.13; 31.15; 31.17.

3) Сравните числа a и b, если известно, что

а) a = b – 0,2; б) в) b + a = 1 + b2.

4) Сравните выражения:

а) (a – 1)(a + 2) и (a + 4)(a – 3); б) a2 + 25 и 10a;

в) (a – 2) 2 и 4(1 – a); г) 1 – a и 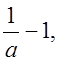где (a > 0).

Р е ш е н и е:

а) (a – 1)(a + 2) и (a + 4)(a – 3);

1 с п о с о б.

a2 + a – 2 и a2 + a – 12;

a2 + a – выражение, которое содержится и в правой части и в левой, по свойствам неравенства уменьшим обе части на данное выражение, получится:

–2 > –12 (верно), значит (a – 1)(a + 2) > (a + 4)(a – 3).

2 с п о с о б.

Найдем разность данных выражений

a2 + a – 2 – (a2 + a – 12) = 10,

так как разность есть число положительное, значит уменьшаемое больше вычитаемого:

(a – 1)(a + 2) > (a + 4)(a – 3)

V. Подведение итогов.

Домашнее задание: прочитать материал параграфа 31, выучить правила данного параграфа. Решить задачи № 31.1; 31.3; 31.16; 31.19.