ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ - урок 4

Цели: повторить понятие квадратного уравнения; повторить различные способы решения квадратных, рациональных и иррациональных уравнений.

Ход урока

I. Организационный момент.

II. Анализ тестирования.

Выставляются оценки за тестирование. Задания, по которым допущено наибольшее количество ошибок, разбираются на доске.

III. Актуализация знаний.

Данные уравнения выписываются на доску или на альбомные листы. Ученики стараются решить уравнения устно, с помощью теоремы, обратной теореме Виета, если учащиеся не справляются, то уравнения решаются на доске.

x2 + x – 2 = 0; x2 – x – 2 = 0; x2 + x – 6 = 0; x2 – x – 6 = 0;

x2 + x – 12 = 0; x2 – x – 12 = 0; x2 + x – 20 = 0; x2 – x – 20 = 0;

x2 + 4x – 21 = 0; x2 + 5x – 14 = 0; x2 – 6x – 7 = 0; x2 – 11x + 10 = 0;

IV. Решение задач.

Необходимо повторить правила решения и оформления следующих заданий:

1) Решить различные уравнения, с полным объяснением на доске:

а) 7x2 + 9x + 2 = 0 с помощью первой формулы дискриминанта;

б) 3x2 + 8x – 9 = 0 с помощью второй формулы дискриминанта;

в) x4 – 26x2 + 25 = 0 – биквадратное уравнение;

г) (x2 + 6x) + 5(x2 + 6x) – 24 = 0 с помощью введения новой переменной;

д) 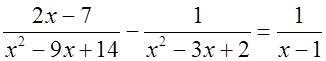– рациональное уравнение;

е) – иррациональное уравнение.

2) Затем выполняются задания из учебника № 25.19; 26.11; 29.26; 30.17.

В классах с высоким уровнем подготовки решаются уравнения № 29.51; 30.21.

3) Повторить правила решения и оформления задач на составление уравнений, выполнив № 25.26; 27.6; 27.21.

V. Подведение итогов.

Домашнее задание: решить задания № 26.8; 27.22, для сильных учеников – 29.52.