Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Решение неравенств второй степени с одной переменной - Неравенства с одной переменной - Уравнения и неравенства с одной переменной
Цель: решение квадратных неравенств.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Решите уравнение ![]()
2. Решите уравнение ![]()
3. При всех значениях параметра а решите уравнение 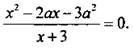
Вариант 2
1. Решите уравнение ![]()
2. Решите уравнение ![]()
3. При всех значениях параметра а решите уравнение ![]()
III. Изучение нового материала
Неравенство вида ах2 + bx + c v 0 (где х - переменная; а, b и с - некоторые числа и а ≠ 0) называют неравенством второй степени с одной переменной, или квадратным неравенством (по аналогии с квадратным уравнением). Подобные неравенства наглядно и удобно решать графически.
Решение сводится к нахождению промежутков х, в которых функция у = ах1 +Ьх + с имеет положительные или отрицательные значения. Для этого надо определить, как расположен график функции у = ах2 + bх + с в координатной плоскости: направление ветвей параболы (вверх или вниз), и найти точки пересечения ее с осью х (если они имеются). Рассмотрим соответствующие примеры.
Пример 1
Решим неравенство 6х2 - х - 1 ≤ 0.
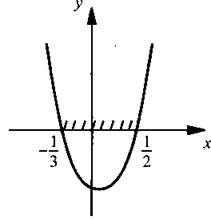
Рассмотрим у = 6х2 - х - 1. Ее графиком является парабола с ветвями, направленными вверх. Найдем точки пересечения параболы с осью абсцисс. Дня этого решим уравнение 6х2 - х - 1 = 0. Его корни х1 = -1/3 и х2 = 1/2. Нарисуем эскиз графика. Видно, что функция принимает неположительные значения на промежутке 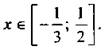 Этот промежуток и является решением данного неравенства.
Этот промежуток и является решением данного неравенства.
Пример 2
Решим неравенство ![]()
Рассмотрим функцию ![]() Ее графиком является парабола с ветвями, направленными вниз. Найдем точки пересечения параболы с осью абсцисс. Для этого решим уравнение
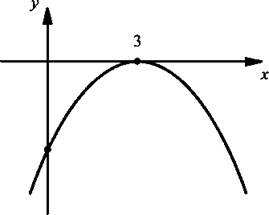
Ее графиком является парабола с ветвями, направленными вниз. Найдем точки пересечения параболы с осью абсцисс. Для этого решим уравнение ![]() Оно имеет единственный корень х = 3. Поэтому парабола касается оси абсцисс в точке х = 3. Нарисуем эскиз графика. Видно, что функция принимает неотрицательные значения (а именно у = 0) только в единственной точке х = 3. Поэтому данное неравенство имеет решение х = 3.
Оно имеет единственный корень х = 3. Поэтому парабола касается оси абсцисс в точке х = 3. Нарисуем эскиз графика. Видно, что функция принимает неотрицательные значения (а именно у = 0) только в единственной точке х = 3. Поэтому данное неравенство имеет решение х = 3.
Из рассмотренных примеров уже можно сформулировать алгоритм решения неравенства ах2 + bх + с v 0:
1. Определяют направление ветвей параболы: при а > 0 - вверх, при а < 0 - вниз.
2. Находят дискриминант D = b2 - 4ас квадратного трехчлена ах2 + bх + с и определяют, имеет ли трехчлен корни.
3. Если трехчлен имеет корни, то отмечают их на оси абсцисс. С учетом направления ветвей строят эскиз параболы, проходящий через построенные на оси х точки.
4. Если трехчлен не имеет корней, строят эскиз параболы, расположенный в верхней полуплоскости при а > 0 и в нижней полуплоскости при а < 0.
5. Находят на оси х промежутки, для которых выполнено данное неравенство.
Разумеется, графический способ может быть использован и для решения более сложных неравенств.
Пример 3
Решим неравенство |х +1|(х - 3) > 0.
Рассмотрим функцию у = |х+1|(х-3) и построим ее график. Для этого раскроем знак модуля, рассмотрев два случая. При х ≥ -1 получаем функцию y = (х + 1)(х - 3). Ее графиком является парабола, направленная ветвями вверх и проходящая через точки x1 = -1 и х2 = 3. Из этой параболы сохраним участок ВС, для которого х ≥ -1.
При х < -1 получаем функцию у = -(х + 1)(х - 3), которая отличается от предыдущей только знаком. Поэтому участок АВ (для х < -1) предыдущей параболы отражаем зеркально вниз и получаем часть BD требуемого графика. Построен график данной функции.
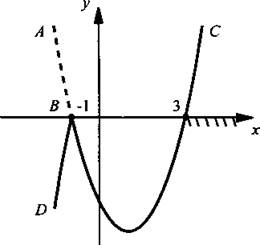
Видно, что данное неравенство (у ≥ 0) выполняется для отдельной точки х = -1 ив промежутке [3; +∞). Поэтому решение неравенства ![]()
Пример 4
Решим неравенство х2 - (а + 4)х + 4а ≤ 0.
Найдем дискриминант квадратного трехчлена D = (а + 4)2 – 4 · 4a = a2 + 8a + 16 - 16а = (a - 4)2 и его корни ![]() т. е. x1 = а и х2 = 4. Поэтому графиком квадратичной функции у = х2 - (а + 4)х + 4а является парабола, направленная ветвями вверх и имеющая с осью абсцисс две или одну общие точки. Значит, необходимо рассмотреть три случая.
т. е. x1 = а и х2 = 4. Поэтому графиком квадратичной функции у = х2 - (а + 4)х + 4а является парабола, направленная ветвями вверх и имеющая с осью абсцисс две или одну общие точки. Значит, необходимо рассмотреть три случая.
а) Пусть x1 < х2, т. е. а < 4. Соответствующий график приведен на рисунке. Видно, что значения функции у ≤ 0 на промежутке [a; 4]. Этот промежуток является решением неравенства в данном случае.
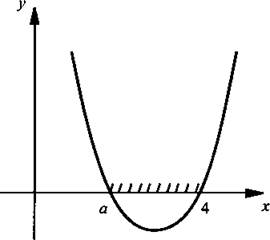
б) Пусть x1 = х2, т. е. а = 4. В этом случае парабола касается оси абсцисс в точке х = 4. Соответствующий график приведен на рисунке. Видно, что значения функции либо положительные, либо их значение равно нулю. Последнее имеет место только в точке х = 4. Эта точка и является решением неравенства в этом случае.
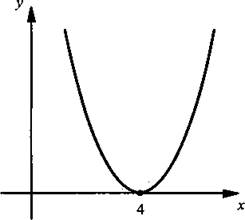
в) Пусть x1 > x2, т. е. a > 4. График приведен на рисунке. Видно, что значения функции y(x) неположительные на промежутке [4; a]. Этот промежуток является решением неравенства для данного случая.
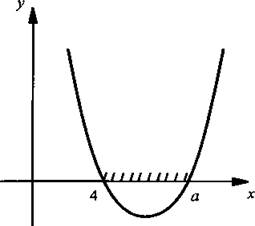
Учитывая три рассмотренные ситуации, запишем окончательный ответ задачи: при а ∈ (-∞; 4) х ∈ [а; 4]; при a = 4 х = 4; при a ∈ (4; +∞) х ∈ [4; a].
IV. Задание на уроке
№ 304 (а, г); 306 (а, б); 308 (б, г); 310 (а); 311 (б); 312 (а, б); 314 (a); 315 (б, в); 318; 320 (а, б); 321 (а).
V. Задание на дом
№ 304 (б, в); 306 (в, г); 308 (а, д); 310 (б); 31 (а); 312 (в, г); 314 (б); 315 (а, д); 319; 320 (в, г); 321 (б).
VI. Подведение итогов урока