Решение неравенств методом интервалов - Неравенства с одной переменной - Уравнения и неравенства с одной переменной

Цель: рассмотреть наиболее удобный и универсальной способ решения неравенств.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (тест).

Вариант 1

1. Решите неравенство 6х2 - 13х + 6 ≤ 0.

Ответы: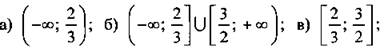

2. Решите неравенство -25х2 + 20х - 4 ≥ 0.

Ответы:

3. Решите неравенство х2 - 3|х| + 2 ≥ 0.

Ответы:

Вариант 2

1. Решите неравенство 15х2 - 34х +15 ≥ 0.

Ответы:

2. Решите неравенство 9х2 -12х + 4 ≤ 0.

Ответы:

3. Решите неравенство х2 - 5|х| + 6 ≥ 0.

Ответы:

III. Изучение нового материала

Рассмотрим наиболее удобный и универсальный способ решения любых неравенств - метод интервалов. Он с успехом может быть использован при решении всех типов неравенств, изучаемых в школе. Пока мы рассмотрим применение этого способа для целых и рациональных неравенств. Суть метода интервалов будет понятна из следующего примера.

Пример 1

Решим неравенство х2 + 2х - 3 ≤ 0.

На числовой оси отметим корни уравнения х2 + 2х - 3 = 0. Это x1 = - 3 и х2 = 1. Эти точки разбили числовую ось на три промежутка: х ∈ (-∞; -3); х ∈ [-3; 1] и х ∈ (1;+∞).

При х ∈ (-∞; -3) в многочлене х2 + 2х - 3 = (х + 3)(х - 1) оба сомножителя отрицательные. Поэтому многочлен х2 + 2х - 3 > 0 (отмечено знаком «+»), и неравенство не выполнено.

Для х ∈ [-3; 1] множитель (х + 3) становится неотрицательным, множитель (х - 1) по-прежнему отрицательный. Поэтому произведение (х + 3)(х - 1) ≤ 0 (отмечено знаком «-»), и неравенство выполнено. Следовательно, интервал х ∈ [-3; 1] удовлетворяет неравенству.

При х ∈ (1; +∞) сомножители (х + 3) и (х - 1) положительные, произведение (х + 3)(х - 1) > 0 (отмечено знаком «+»), и неравенство не выполнено.

Заметим, что столь детальный анализ знаков при решении квадратных неравенств является излишним. Достаточно определить знак выражения х2 + 2х - 3 в одной точке, не совпадающей с границами интервалов (например, при х = -10 выражение х2 + 2х - 3 = (-10)2 + 2(-10) - 3 = 77 > 0). Кроме того, надо учесть, что при переходе к каждому следующему промежутку знак выражения х2 + 2х - 3 меняется на противоположный. Поэтому диаграмма знаков, приведенная на рисунке, может быть получена сразу (решение неравенства отмечено штриховкой).

Пример 2

Решим систему неравенств

Для решения используем аналитический (метод интервалов) и графический способы.

а) Решим сначала первое неравенство х2 + 4х + 3 ≤ 0. Найдем корни соответствующего уравнения х2 + 4х + 3 = 0. Это х = - 3 и x2 = -1. Нанесем эти точки на числовую ось, которые разбивают ее на три интервала. Определим знак выражения х2 + 4х + 3, например, при х = 0: 02 + 4 · 0 + 3 = 3 > 0. После этого легко нарисовать диаграмму знаков рассматриваемого выражения. Видно, что неравенство выполняется при х ∈ [-3; -1].

Теперь рассмотрим второе неравенство х2 + 3х + 2 ≥ 0. Корни этого выражения x1 = -2 и х2 = -1. Наносим эти точки на числовую ось. Определяем знак выражения х2 + 3х + 2, например, при х = 5: 52 + 3 · 5 + 2 = 42 > 0. Рисуем диаграмму знаков для этого выражения. Видно, что неравенство выполняется для х ∈ (-∞; -2]U[-1; +∞).

Найдем те значения х, при которых выполнены оба неравенства. Для этого еще раз нанесем решения первого (штриховка сверху) и второго (штриховка снизу) неравенств на числовую ось. Видно, что оба неравенства выполнены для промежутка х ∈ [-3; - 2] ив отдельной точке х = -1.

Итак, решение данной системы неравенств х ∈ [-3; - 2]U{-1}.

б) Построим графики функций у1 = х2 + 4х + 3 и у2 = х2 + 3х + 2.

Видно, что неравенство х2 + 4х + 3 ≤ 0 (график у1 находится не выше оси абсцисс) выполнено для х ∈ [-3; -1]. Неравенство х2 + 3х + 2 ≥ 0 (график у2 находится не ниже оси абсцисс) выполнено при х ∈ (-∞;-2]U[-1;+∞). Оба неравенства выполнены для х ∈ [-3; -2]U{-1}.

Рассмотрим более сложные задачи по этой теме.

Пример 3

Решим неравенство |5 - х|(х - 1) + 5 < х.

Решим это неравенство аналитически и графически.

а) Перенесем все члены неравенства в левую часть: |5 - х|(х - 1) + 5 - х < 0 и раскроем знак модуля.

Если 5 - х ≥ 0 (т. е. х ≤ 5), то получаем неравенство (5 - х)(х - 1) + (5 - х) < 0, или (5 - х)(х - 1 + 1) < 0, или (5 - х)х < 0. Решаем это неравенство методом интервалов. Наносим корни соответствующего уравнения: х1 = 0 и х2 = 5. Определяем знак выражения (5 - х)х, например, для х = 2: (5 - 2) · 2 = 6 > 0. После этого рисуем диаграмму знаков.

Решением неравенства является х ∈ (-∞; 0)U(5; +∞). Так как рассматривается область х ≤ 5, то решением является промежуток х ∈ (-∞; 0).

Если 5 - х < 0 (т. е. х > 5), то имеем неравенство -(5 - х)(х - 1) + (5 - х) < 0, или (5 – х)(-х + 1 + 1) < 0, или (5 - х)(2 - х) < 0. На числовой оси отмечаем корни соответствующего уравнения: х1 = 2 и х2 = 5. Находим знак выражения (5 - х)(2 - х), например, при х = 3: (5 - 3)(2 - 3) = -2 < 0 и рисуем диаграмму знаков.

Решением неравенства будет интервал х ∈ (2; 5). Так как рассматривается область х > 5, то этот промежуток решением данного неравенства не является.

Итак, решение неравенства х ∈ (-∞; 0).

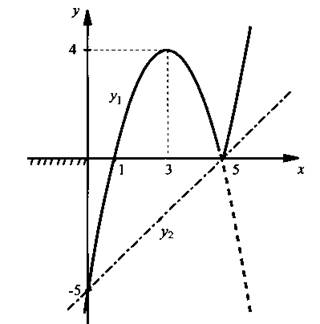
б) Запишем данное неравенство в виде |5 - х|(х - 1) < х - 5. Построим график функции у1 = |5 - х|(х - 1). Для этого раскроем знак модуля. При х ≤ 5 получаем: у1 = (5 - х)(х - 1). В этой области построим график такой функции. Для х > 5 имеем: у1 = -(5 - х)(х - 1). Видно, что эта функция отличается от предыдущей только знаком минус. Поэтому этот график легко получить из предыдущего, если отразить пунктирную часть параболы относительно оси абсцисс зеркально вверх.

Построим также график функции у2 = х - 5. Теперь необходимо определить, при каких значениях х значение функции у2 больше значения функции у1 (т. е. графику находится выше у1). Из рисунка видно, что это происходит при х ∈ (-∞; 0).

Пример 4

Решим неравенство х2 - (b + 4)х + 4b ≥ 0.

Найдем дискриминант соответствующего уравнения: Теперь легко определить и корни: или х1 = b и х2 = 4. Параметр b может быть меньше числа 4, совпасть с ним или оказаться больше числа 4. Рассмотрим эти случаи.

а) Если b < 4, то диаграмма знаков изображена на рисунке. Неравенству удовлетворяют промежутки, расположенные за корнями, т. е. х ∈ (-∞; b]U[4; +∞).

б) Если b = 4, то неравенство имеет вид: х2 - 8х + 16 ≥ 0, или (х - 4)2 ≥ 0. Это неравенство выполнено при всех х е (-∞; +∞).

в) Если b > 4, то неравенству удовлетворяют интервалы, расположенные за корнями, т. е. х ∈ (-∞; 4]U[b; +∞).

Итак, получаем ответ: для b ∈ (-∞; 4) х ∈ (-∞; b]U[4; +∞); для b = 4 х ∈ (-∞; +∞); для b ∈ (4; +∞) х ∈ (-∞; 4]U[b; +∞).

Заметим, что эти три случая можно объединить, если использовать метод интервалов на координатной плоскости (а не на координатной прямой, как ранее). Такой подход особенно удобен при решении сложных задач.

На координатной плоскости bОх построим корни х1 = b и х2 = 4 квадратного трехчлена. Очевидно, что данное неравенство х2 - (b + 4)х + 4b ≥ 0 выполняется на промежутках х, расположенных за корнями х1 и х2 квадратного трехчлена. Множество таких точек (b; х) заштриховано. Если зафиксировать значение b и провести вертикальную прямую х = b, то видно, что штрихпунктирная линия попадает в заштрихованную область на промежутках х ∈ (-∞; 6]U[4; +∞). Эти промежутки являются решением неравенства при b < 4. Аналогично получаем решения неравенства при b = 4 и b > 4.

Пример 5

Найти все значения а, при которых один из корней уравнения х2 - 2х - а2 = 0 меньше (-1), а другой - больше 1.

Найдем дискриминант этого уравнения: D = 22 – 4 · (-а2) = 4 + 4а2. При всех значениях а величина D > 0, поэтому уравнение имеет два различных корня. Схематично изобразим график функции у = х2 - 2х - а2. Вершина этой параболы находится в точке (1; -1 - а2). Тогда больший корень х2 всегда больше 1. Для того чтобы меньший корень х1 был меньше (-1), необходимо и достаточно, чтобы значение функции у при х = -1 было отрицательным.

Запишем это условие: (-1)2 - 2(-1) - а2 < 0 или 3 - а2 < 0. Решим это неравенство методом интервалов. Находим корни соответствующего уравнения: При а = 0 определяем знак этого выражения: 3 - 02 = 3 > 0 и рисуем диаграмму знаков. Теперь можно записать ответ: при условия задачи выполнены.

IV. Задание на уроке

№ 325 (а, г); 326 (б, в); 330 (а, б); 331 (а, в); 332 (а).

V. Задание на уроке

№ 325 (б, в); 326 (а, г); 330 (в, г); 331 (б, г); 333 (а).

VI. Подведение итогов урока