Вариант № 8 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. В упаковке 16 пачек сахара. За день кондитерская фабрика расходует 183 пачки. Какое наименьшее количество упаковок сахара нужно купить фабрике на 15 дней?

В2. На рисунке 56 показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 8 августа. Ответ дайте в градусах Цельсия.

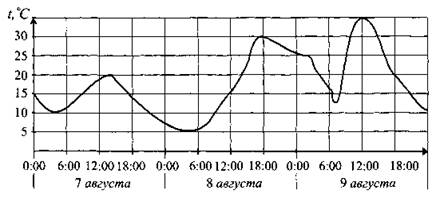
Рис. 56.

В3. Найдите площадь трапеции, вершины которой имеют координаты (3; 1), (8; 4), (10; 4), (10; 1) (см. рис. 57).

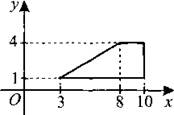
Рис. 57.

В4. В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трёх городах России (по данным на начало 2011 года).

Наименование продукта	Астрахань	Новочеркасск	Омск
Пшеничный хлеб	14	15	18
Картофель (1 кг)	30	35	40
Рис (1 кг)	40	50	35
Колбаса(1 кг)	260	250	240
Сыр (1 кг)	240	220	230
Подсолнечное масло (1 литр)	42	45	40

Определите, в каком из этих городов окажется самым дешёвым следующий набор продуктов: 3 кг картофеля, 1 кг колбасы, 2 литра подсолнечного масла. В ответе запишите стоимость данного набора продуктов в этом городе (в рублях).

В5. Найдите корень уравнения

В6. В треугольнике АВС угол С равен 90°, СВ = 8, cos В = 2√5/5. Найдите АС.

В7. Найдите значение выражения

В8. На рисунке 58 изображён график у = f'(x) производной функции f(x) и отмечены девять точек на оси абсцисс: x₁, x₂, x₃, ..., x₉. Сколько из этих точек принадлежат промежуткам убывания функции f(x)?

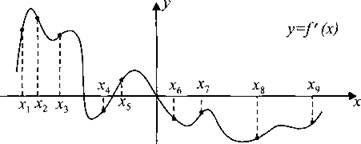
Рис. 58.

В9. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса (см. рис. 59). Радиус сферы равен 3√2. Найдите образующую конуса.

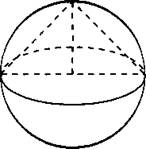
Рис. 59.

В10. Вероятность того, что батарейка бракованная, равна 0,1. Покупатель в магазине выбирает случайную упаковку, в которой две батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

В11. Найдите площадь поверхности многогранника, изображённого на рисунке 60 (все двугранные углы прямые).

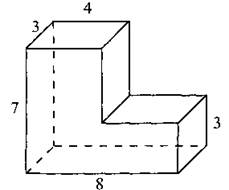
Рис. 60.

В12. К источнику с ЭДС Ε = 100 В и внутренним сопротивлением r = 1 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задаётся формулой При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 80 В? Ответ выразите в омах.

В13. Автомобилист проехал расстояние между двумя городами за 3 дня. В первый день он проехал 1/4 всего пути и ещё 40 км, во второй он проехал 1/3 всего пути и ещё 30 км, а в третий день он проехал 17/60 всего пути и оставшиеся 45 км. Найдите расстояние между городами (в км).

В14. Найдите точку минимума функции у = (5 — х)е^{5 - x}.

Часть 2

С1. а) Решите уравнение б sin² х + 2 sin² 2х = 5.

б) Найдите корни этого уравнения, принадлежащие промежутку (π/2; 3π/2).

С2. Основанием пирамиды служит равнобедренный треугольник, один из углов которого равен 60°. Высота пирамиды равна 4, а боковые рёбра наклонены к плоскости основания под углом 45°. Найдите объём пирамиды.

С3. Решите систему неравенств

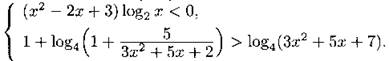
С4. В параллелограмме MNPQ диагональ МР равна 7, а диагональ NQ равна 5. На МР выбрана точка Е таким образом, что вокруг четырёхугольника NPQE можно описать окружность. Найдите длину NK, где К — центр окружности, описанной около треугольника MEQ, и sin ∠MQE = 1/2.

С5. При каких значениях а уравнение имеет решения на промежутке [8; 9]?

С6. Найдите натуральное число а в каждом из следующих случаев: а) если к десятичной записи числа а справа приписать цифру 6, то получится 4а²;

б) если к десятичной записи числа а приписать справа одну из цифр, а затем из получившегося числа вычесть а², то получится 8а; в) если к десятичной записи числа а справа приписать некоторые четыре цифры, то получится а⁶.