Вариант № 24 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Железнодорожный билет для взрослого стоит 1580 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 17 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?

В2. На диаграмме 138 показана среднесуточная температура воздуха в городе Ростове-на-Дону с 15 по 27 ноября 2010 года. По горизонтали указываются даты, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднесуточную температуру в Ростове-на-Дону в период с 21 по 27 ноября 2010 года включительно. Ответ дайте в градусах Цельсия.

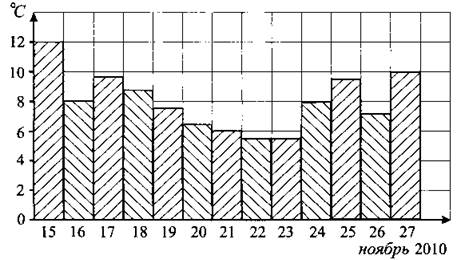
Рис. 138.

В3. Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты A(1;5), В(5; 5), C(5; —1) (см. рис. 139).

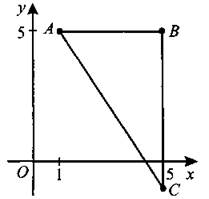
Рис. 139.

В4. Клиент хочет арендовать автомобиль на двое суток для поездки протяжённостью 1500 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды. Помимо аренды, клиент обязан оплатить стоимость топлива для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешёвый вариант?

Автомобиль	Топливо	Расход топлива (л на 100 км)	Арендная плата (руб. за 1 сутки)
А	Дизельное	8	3500
Б	Бензин	11	3300
В	Газ	14	3000

Цена дизельного топлива — 20 рублей за литр, бензина — 22 рубля за литр, газа — 15 рублей за литр.

В5. Найдите корень уравнения log₂ (6 — х) = log₄ х. Если уравнение имеет более одного корня, то укажите меньший из них.

В6. Три стороны описанного около окружности четырёхугольника относятся (в последовательном порядке) как 9:4:5. Найдите большую сторону этого четырёхугольника, если известно, что его периметр равен 98.

В7. Найдите 8х - 27у + 68, если

В8. На рисунке 140 изображён график некоторой функции у = f(x). Функция F(x) = —х³ + 18х² — 81x + 214 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

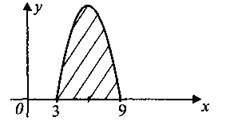
Рис. 140.

В9. В основании прямой призмы лежит прямоугольный треугольник с катетами 7 и 4√2. Боковые рёбра равны 4/π. Найдите объём цилиндра, описанного около этой призмы.

В10. Чтобы пройти в следующий круг соревнований, шахматисту нужно набрать хотя бы 1,5 очка по итогам двух игр. Если шахматист выигрывает, он получает 1 очко, в случае ничьей — 0,5 очка, если проигрывает — 0 очков. Найдите вероятность того, что шахматисту удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятность выигрыша и проигрыша одинакова и равна 0,3.

В11. Диаметр основания конуса равен 12, а угол при вершине осевого сечения 90° (см. рис. 141). Вычислите объём конуса, делённый на π.

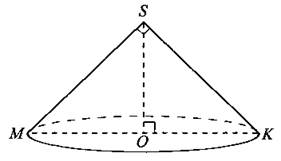
Рис. 141.

В12. В ходе распада радиоактивного изотопа его масса уменьшается по закону m(t) = m₀ ∙ 2^-t/T, где m₀ (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, Т (мин) — период полураспада. В начальный момент времени масса изотопа то = 150 мг. Период его полураспада Т = 3 мин. Через сколько минут масса изотопа будет равна 18,75 мг?

В13. Весной катер идёт по течению в 1,8 раза быстрее, чем против течения. Летом течение становится на 0,5 км/ч медленнее, поэтому летом катер идёт по течению в 5/3 раз быстрее, чем против течения. Определите собственную скорость катера (в км/ч).

В14. Найдите точку минимума функции у = (х — 3)²(х + 4) — 2.

Часть 2

С1. Решите уравнение х⁴ - 10х³ + 35х² — 50x + 24 = 0.

С2. В правильной треугольной призме с площадью основания S₀ = 3 через сторону нижнего основания и противоположную вершину верхнего основания проведено сечение, площадь которого S_c = 5. Найдите расстояние от вершины основания, через которую не проходит сечение, до плоскости сечения.

С3. Решите неравенство 18 arccos² х + 27π rarcsin x — 6,5π² ≤ 0.

С4. Найдите стороны треугольника с наименьшей площадью, у которого одна из сторон равна 6, а радиус вписанной окружности равен 2.

С5. Определите значения параметра а, при которых число а лежит между корнями уравнения а²х² + (7а — 6а²)x + 6а — 8 = 0.

С6. Дана сумма п слагаемых

Найдите:

а) сумму четырёх слагаемых S₄;

б) все такие натуральные значения n, при которых S_n ≥ 1/9;

в) все такие натуральные значения n, при которых S_n ≤ 1/10;

г) все такие натуральные значения n, при которых