Вариант № 27 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Аня купила проездной билет на месяц и сделала за месяц 55 поездок. Сколько рублей она сэкономила, если проездной билет стоит 400 рублей, а разовая поездка составляет 2,5% от стоимости проездного билета?

В2. На рисунке 152 показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указываются дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку, на сколько градусов Цельсия наибольшая температура 13 мая превышала наибольшую температуру 11 мая.

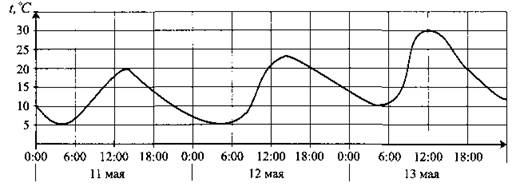
Рис. 152.

В3. Стороны параллелограмма равны 15 и 10. Высота, опущенная на большую сторону, равна 6. Найдите высоту, опущенную на меньшую сторону параллелограмма (см. рис. 153).

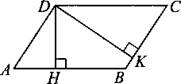
Рис. 153.

В4. Строительный подрядчик планирует купить 15 тонн облицовочного кирпича у одного из трёх поставщиков. Вес одного кирпича 5 кг. Цены и условия доставки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?

Поставщик	Стоимость кирпича (руб. за штуку)	Стоимость доставки (руб.)	Специальные условия
А	16	6000	При стоимости заказа свыше 40 000 рублей предоставляется скидка 8%, а доставка осуществляется бесплатно
Б	15	10000	При заказе на сумму свыше 25 000 рублей доставка со скидкой 70%
В	17	3500	За каждые 90 оплаченных кирпичей — 10 кирпичей в подарок. При заказе на сумму свыше 42 000 рублей доставка осуществляется бесплатно

В5. Найдите корень уравнения В ответе запишите корень уравнения или их сумму, если корней несколько.

В6. Острый угол прямоугольного треугольника равен 36° (см. рис. 154). Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Рис. 154.

В7. Найдите значение выражения если log_b а = 1,5.

В8. Прямая у = —4х + 1 является касательной к графику функции у = х³ + 5x² + 3x + 4. Найдите абсциссу точки касания.

В9. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ ребро АВ = 4, ребро = 8, ребро АА₁ = 6. Найдите площадь сечения, проходящего через точки А₁, D₁ и М, если точка М — середина ребра ВВ₁.

В10. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Вероятность попадания по цели при первом выстреле равна 0,3, а при каждом последующем — 0,7. Сколько выстрелов потребуется сделать для того, чтобы вероятность хотя бы одного попадания по цели была не менее 0,97?

В11. Найдите объём правильной шестиугольной призмы (см. рис. 155), стороны основания которой равны 4, а боковые рёбра равны 2√3.

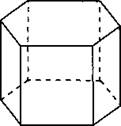
Рис. 155.

В12. Для обогрева помещения, температура в котором равна Т_п = 20°С, через радиатор отопления пропускают горячую воду температурой T_B = 84°С. Расход проходящей через трубу воды m = 0,5 кг/с. Проходя по трубе расстояние х (м), вода охлаждается до температуры Т(°С), причём (м), где — теплоёмкость воды, — коэффициент теплообмена, a α = 0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 49 м?

В13. Свежий плод инжира содержит 70% воды, а плод сушёного инжира — 3,4%. Сколько килограммов инжира потребуется для получения 10 кг сушёного инжира?

В14. Найдите наименьшее значение функции у = log₃(x² + 2х + 4) + 3.

Часть 2

С1. а) Решите уравнение

б) Найдите его корни, удовлетворяющие условию 0 < х < 4π/3.

С2. Для рёбер правильной треугольной призмы АВСА₁В₁С₁ выполняется равенство Найдите угол между прямыми АВ₁ и ВС₁.

С3. Решите неравенство

С4. Площадь треугольника АВС равна 15√2, сторона АВ равна 5,5, медиана ВМ равна 5. Найдите АС.

С5. Найдите все значения а, при которых расстояние между корнями уравнения х² + (а — 34)x — 35а — 36 = 0 будет минимальным, а само уравнение имеет ровно 2 корня.

С6. Найдите все пары целых чисел х и у, которые удовлетворяют уравнению 3ху + 14x + 17у + 71 = 0.