Вариант № 28 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Цена на холодильник была повышена на 12% и составила 14000 рублей. Сколько рублей стоил холодильник до повышения цены?

В2. На рисунке 156 показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшим и наименьшим значениями температуры воздуха 8 августа. Ответ дайте в градусах Цельсия.

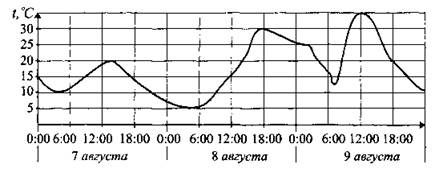
Рис. 156

В3. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов (см. рис. 157).

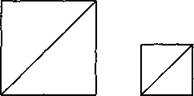
Рис. 157

В4. Коля загружает на свой компьютер из Интернета файл размером 46 Мб за 40 секунд. Петя загружает файл размером 66 Мб за 60 секунд, а Миша загружает файл размером 27 Мб за 24 секунды. Сколько секунд будет загружаться файл размером 529 Мб на компьютер с наибольшей скоростью загрузки?

В5. Найдите корень уравнения Если уравнение имеет более одного корня, то укажите наибольший из них.

В6. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 5:6, считая от вершины тупого угла (см. рис. 158). Найдите большую сторону параллелограмма, если его периметр равен 68.

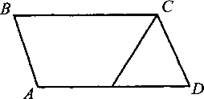
Рис. 158.

В7. Найдите значение выражения (2 — log₅ 250)(2 + log₁₀ 0,05).

В8. Прямая у = —7х + 3 является касательной к графику функции у = ах² + 3х — 2. Найдите а.

В9. От треугольной призмы, объём которой равен 18, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объём оставшейся части.

В10. Чтобы поступить в институт на специальность «Архитектура», абитуриент должен набрать на ЕГЭ не менее 75 баллов по каждому из трёх предметов — математике, русскому языку и истории. Чтобы поступить на специальность «Телевидение», нужно набрать не менее 75 баллов по каждому из трёх предметов — русскому языку, литературе и истории. Вероятность того, что абитуриент К. получит не менее 75 баллов по математике, равна 0,6, по русскому языку — 0,8, по истории — 0,5 и по литературе — 0,7. Найдите вероятность того, что К. сможет поступить хотя бы на одну из двух упомянутых специальностей.

В11. Диагональ прямоугольного параллелепипеда равна 6√2 и образует углы 30°, 30° и 45° с плоскостями граней параллелепипеда (см. рис. 159). Найдите объём параллелепипеда.

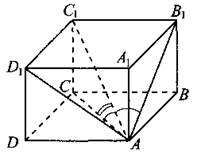
Рис. 159.

В12. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 50 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние d₂ от линзы до экрана — в пределах от 200 до 250 см. Изображение на экране будет чётким, если выполнено соотношение Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.

В13. Десятого января все книги в магазине подешевели на некоторое число процентов, а спустя несколько дней подорожали на то же самое число процентов от установившейся цены. В результате цены стали на 0,25% меньше, чем до десятого января. На сколько процентов подешевели книги 10 января?

В14. Найдите наибольшее значение функции у = log₃(18 + 6x — х²) + 4.

Часть 2

С1. а) Решите уравнение

б) Найдите его корни, удовлетворяющие условию 0 < х < 3π/2.

С2. В основании пирамиды МАВС лежит прямоугольный треугольник АВС. Боковое ребро МВ перпендикулярно плоскости основания и АС = ВС. На ребре МС взята точка К — середина этого ребра. Найдите угол между плоскостями ВАК и АКС, если МВ = АС.

С3. Решите неравенство

С4. Диагональ равнобедренной трапеции равна 5, а площадь равна 12. Найдите высоту трапеции.

С5. Вычислите отрицательный коэффициент 6 и корни уравнения х² + bх — 1 = 0, если известно, что с увеличением каждого из этих корней на единицу они становятся корнями уравнения х² — b²х — 6 = 0.

С6. Решите уравнение 1! + 2! + ... + n! = m², где n ∈ N, m ∈ Z.