Вариант № 29 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Студент получил гонорар в размере 1200 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 50 рублей за штуку и букет должен состоять из нечётного числа цветов?

В2. На графике 160 показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали — удельная теплоёмкость в Определите по рисунку, при какой наибольшей температуре удельная теплоёмкость раствора составит не более 4200 Ответ дайте в градусах Цельсия.

Рис. 160.

В3. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность (см. рис. 161)?

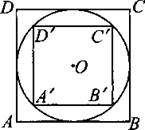
Рис. 161.

В4. Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 7 кубометров пеноблоков и 3 мешка цемента. Для бетонного фундамента необходимо 6 тонн щебня и 50 мешков цемента. Кубометр пеноблоков стоит 2900 рублей, щебень стоит 750 рублей за тонну, а мешок цемента стоит 280 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешёвый вариант?

В5. Найдите корни уравнения В ответе запишите наименьший положительный корень.

В6. В прямоугольнике расстояние от точки пересечения диагоналей до большей стороны меньше расстояния до меньшей стороны на 4. Его периметр равен 52. Найдите меньшую сторону прямоугольника.

В7. Найдите частное g(а) : g(1/a), если

В8. Прямая у = — 7х + 11 является касательной к графику функции у = 2х² — 5x + с. Найдите с.

В9. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра равны 3. Найдите расстояние между вершинами А и Е₁.

В10. В Волшебной стране бывает два типа погоды: ясная и дождливая, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,6 погода завтра будет такой же, как и сегодня. Сегодня 11 мая, погода в Волшебной стране дождливая. Найдите вероятность того, что 14 мая в Волшебной стране будет ясная погода.

В11. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 3√3, а высота равна 7 (см. рис. 162).

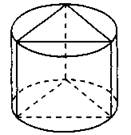
Рис. 162.

В12. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U₀cos(ωt + φ), где t — время в секундах, амплитуда U₀ = 30 В, частота ω = 80°/с, фаза φ = 30°. Датчик настроен так, что если напряжение в нём не ниже чем 15 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

В13. Компания «Омега-транс» начала инвестировать средства в перспективную отрасль в 2003 году, имея капитал в размере 10000 долларов. Каждый год, начиная с 2004 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания «Елена-плюс» начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 5000 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний (более успешной) был больше капитала другой компании к концу 2008 года, если прибыль из оборота не изымалась?

В14. Найдите наибольшее значение функции на отрезке [-2π/3; 0].

Часть 2

С1. Решите уравнение

С2. В треугольной пирамиде SABC SC = 10, С — проекция вершины S на плоскость основания, АС = √21, ВС = 2√11, АВ = 6. Точки М и Р — середины рёбер SA и SB соответственно. Найдите площадь сечения, проходящего через точки М, Р, С.

С3. Решите систему неравенств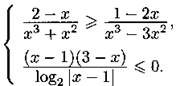

С4. Окружность радиуса 13 вписана в угол 60°. Вторая окружность также вписана в этот угол и пересекается с первой в точках А и В. Известно, что АВ = 10. Найдите расстояние между центрами окружностей.

С5. Найдите все значения параметра а, при каждом из которых уравнение имеет два решения.

С6. Решите уравнение в натуральных числах: 3^m + 7 = 2ⁿ.