Комбинированные уравнения - Урок 2 - Уравнения. Системы уравнений - Алгебра и начала анализа - Повышенный уровень 3

1273. При каких значениях параметра а один из корней уравнения принадлежит отрезку [—1; 1].

1274. Даны два уравнения: и Значение параметра p выбирается таким образом, что число различных корней второго уравнения в сумме с числом р + 1 даёт число различных корней первого уравнения. Найдите все значения параметра р ≠ —2, удовлетворяющие условию, и сумму корней первого уравнения при каждом значении параметра, выбранном таким образом.

1275. Даны два уравнения: и Значение параметра р выбирается так, что оба уравнения имеют смысл и число 0,5(р + 2) равно произведению числа различных корней первого уравнения и числа различных корней второго уравнения. Решите второе уравнение при каждом значении параметра, выбранном таким образом.

1276. Найдите количество всех решений системы уравнений

1277. Найдите количество всех решений системы уравнений

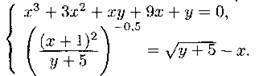
Решите систему уравнений (1278—1281):

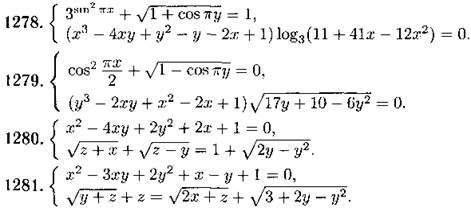
1282. Найдите число решений системы

1283. Сколько решений имеет система уравнений?

1284. Сколько решений имеет следующая система уравнений?

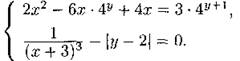
1285. Найдите количество решений системы уравнений

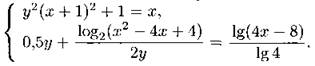
1286. Решите систему уравнений

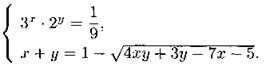
1287. Докажите, что система уравнений 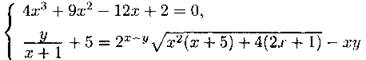имеет два решения.

1288. Докажите, что система уравнений имеет единственное решение.

1289. Определите количество решений системы уравнений

1290. Решите систему уравнений

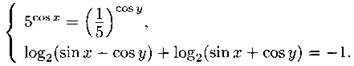
1291. Найдите количество решений системы уравнений

1292. Решите систему уравнений

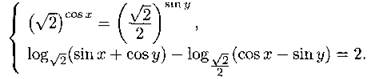
1293. Найдите количество всех решений системы уравнений

Решите уравнение (1294—1296):

1294. f(g(x) + 1) — g(f(x) + 3) = 6, если f(x) = х⁴ — 32x + 50,

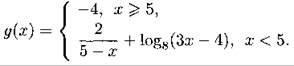
1295. f(g(x)) + g(1 - f(x)) = f(x) + 2, если известно, что и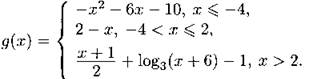

1296. g(f(x) — 44) + f(g(x)) = 8, если известно, что f(x) = -x⁶ + 32x + 5 и

1297. Для чисел a₁, a₂, ..., а₄₀ верны условия a_n+1 = f(а_n), а_n > 0, n = 1, 2, ..., 39. Найдите a₅ + а₈ + а₁₁, если известно, что а₄₀ = 1 и

1298. Для чисел a₁, a₂, ..., а₉₉ верны равенства a_n+1 = f(a_n), n = 1, 2, ..., 98. Найдите а₃₃ + а₄₀, если известно, что а₉₉ = 0, а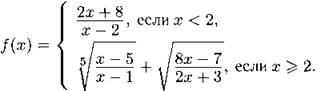

1299. Для чисел а₁, а₂, ..., а₂₆ верны равенства a_n+1 = f(a_n), n = 1, 2, ..., 25. Найдите a₃ + a₄ + a₅, если известно, что a₂₆ = 0 и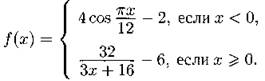

1300. Для чисел а₁, а₂, ..., а₃₀ верны равенства a_n+1 = f(a_n), n = 1, 2, 3, ..., 29. Найдите 7_a9 — 2_a17, если известно, что a₃₀ = 2, а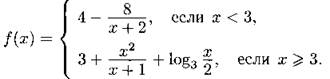

Решите уравнение (1301—1304):

1301. f(g(x)) + g(f(x) + f(-x)) = 5, где f(x) = 3^x + 2x - ln5,

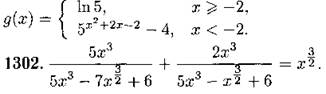
1305. Найдите значения а, при которых уравнение имеет единственное решение.

1306. Известно, что уравнение рх² + (р + 3)x + 4 = 0 имеет хотя бы один корень. Найдите все значения параметра р, при которых число различных корней этого уравнения равно числу различных корней уравнения

1307. При каких значениях параметра а уравнение x² — 2a sin(соs x) + а² sin 2 = 0 имеет единственное решение?

1308. При каких значениях параметра b уравнение b⁴ — 8b cos(cos x) — 9x² = 0 имеет единственное решение?

1309. Решите систему уравнений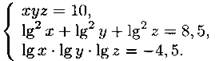

1310. При каких значениях параметра k уравнение имеет ровно один корень.

1311. При каких значениях параметра а уравнение имеет единственное решение?

1312. При каких значениях параметра а уравнение имеет единственное решение?

1313. При каких положительных значениях параметра а модуль разности корней уравнения ах² + 2x — 2,25 = 0 не больше расстояния между точками экстремума функции f(x) = 2x³ — 9x² — 6аx + 13а²?

1314. При каких положительных значениях параметра а расстояние между точками экстремума функции f(x) = x³ + 6x² — 9аx + 4а² не превосходит удвоенного модуля разности корней уравнения

1315. Найдите все значения а, при которых каждое из уравнений имеет хотя бы один корень.

1316. Найдите все значения а, при которых ни одно из уравнений не имеет решений.

1317. Найдите все значения а, при каждом из которых наименьшее значение функции f(x) = ах + 6 + | —x² — 6x — 5| больше 2.

1318. Найдите все значения а, при каждом из которых наименьшее значение функции f(x) = 2ax + 5 + │х² + 6x + 5| меньше 1.

1319. Найдите все значения а, при каждом из которых функция f(x) = х² — 5│х — а²│ — 13х имеет хотя бы одну точку максимума.

1320. Найдите все значения а, при каждом из которых функция f(x) = х² + 5│х — а²│ — 13х имеет хотя бы одну точку максимума.

1321. Найдите все значения а, при каждом из которых наименьшее значение функции f(x) = 4ах + │х² — 8х + 15│ меньше 1.

1322. Найдите все значения а, при каждом из которых наибольшее значение функции f(x) = 4ax + │x² — 8x + 15| на отрезке [2,75; 5,25] меньше 1.

1323. Найдите все значения а, при каждом из которых функция f(x) = х² — 2│х — а²│ — 3х имеет хотя бы одну точку максимума.

1324. Найдите все значения а, при каждом из которых функция f(x) = х² — 2│х — а²│ — 3х имеет хотя бы одну точку минимума.

1325. Найдите все значения а, при которых уравнение имеет корни и все корни неотрицательны.

1326. Найдите все значения параметра а, при которых уравнение имеет корни.

1327. Найдите все значения а, для которых при каждом х из промежутка [4; 16] значение выражения не больше значения выражения (а + 2) log₂ х.

1328. Найдите все значения а, для которых при каждом х из промежутка [3; 9] значение выражения не больше значения выражения (a + 1) log₃ х.

1329. Найдите все значения параметра а, при каждом из которых неравенство выполняется при всех значениях х, таких, что 2 ≤ х ≤ 3.

1330. Найдите все значения параметра а, при каждом из которых неравенство выполняется при всех значениях х, таких, что —1 ≤ х ≤ 1.

1331. При каких значениях параметра а система имеет единственное решение?

1332. При каких значениях параметра а система не имеет решений?

1333. Найдите значения параметра а, при которых разрешимо неравенство

1334. Найдите значения параметра а, при которых разрешимо неравенство

1335. Решите уравнение

1336. Решите уравнение

1337. Найдите все значения параметров а и b, при которых уравнения 2x² — аx — 8 = 0 и x³ + bх — 16 = 0 имеют два общих корня, и найдите эти корни.

1338. Найдите все значения параметров а и b, при которых уравнения 3x³ + 6x² — 25 = 0 и х³ — ах + 15 = 0 имеют два общих корня, и найдите эти корни.

1339. Найдите все значения параметра а, при каждом из которых ровно одно решение неравенства 4х² — 4х — а² + 4а ≤ 3 удовлетворяет неравенству ах(а — 2 + х) ≥ 0.

1340. Найдите все значения а, при каждом из которых ровно одно решение неравенства x² + (10 + 3а)x + 2а² + 12а + 16 ≤ 0 удовлетворяет неравенству ах(х — 8 — а) ≤ 0.

1341. Найдите все значения параметра а, при каждом из которых неравенство е^х-а-2 + х² ≤ а — 5х имеет единственное решение.

1342. Найдите все значения параметра b, при каждом из которых неравенство е^х+b+3 + х² ≤ b — 3х имеет единственное решение.

1343. Найдите все значения а, при которых неравенство выполняется для всех х ∈ (—2; 1).

1344. Найдите все значения а, при которых неравенство выполняется для всех х ∈ (—1; 1).

1345. Найдите все положительные значения а, при которых система имеет единственное решение.

1346. Найдите все положительные значения а, при которых система имеет единственное решение.

1347. Найдите все значения параметра а, при каждом из которых система имеет ровно три различных решения.

1348. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно два решения.

1349. Найдите все значения параметра а, при каждом из которых система имеет ровно 4 решения.

1350. Найдите все значения параметра а, при каждом из которых система имеет ровно 4 решения.

1351. Дан многочлен f(x) = x² + │m — 2│х + 5 — 2m. Известно, что Найдите все значения параметра m, при которых число корней хотя бы двух из уравнений f(x) = 0, g₁(x) = 0 и g₂(x) = 0 будет различным.

1352. Дан многочлен f(x) = x² — |3 — m|x — m + 4. Известно, что Найдите все значения параметра m, при которых число корней хотя бы двух из уравнений f(x) = 0, g₁(x) = 0 и g₂(x) = 0 будет различным.

1353. Найдите все значения а, при каждом из которых система имеет решение.

1354. Найдите все значения а, при каждом из которых система имеет решение.

1355. Для каждого значения а решите уравнение

1356. Найдите все значения параметра а, при которых система уравнений имеет ровно 2 решения.

1357. Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два корня.

1358. Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два корня.

1359. При каких значениях а уравнение имеет только один корень?

1360. При каких значениях b уравнение имеет только один корень?

1361. При каких значениях параметра а уравнение имеет единственное решение?

1362. При каких значениях параметра р существует хотя бы одно число х из отрезка [2; 3], удовлетворяющее условию