Поурочные разработки по геометрии 10 класс
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» - ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цель урока:
- проконтролировать знания, умения и навыки по данной теме.
Ход урока
I. Организационный момент
II. Контрольная работа (см. приложение)
I уровень
Ответы к задачам:
№ 1. да. № 2. б) 6 см. № 3. б) 45°. |
№ 1. да. № 2. б) 8 см. № 3. б) 60°. |
II уровень
Ответы к задачам:
№ 1 а) да; б) нет; в) да. № 2 б) 6 см; 10 см. № 3 б) 50°. |
№ 1 а) нет; б) да; в) да. № 2 б) 6 см; 10 см. № 3 б) 45°. |
III уровень
Ответы к задачам:
№ 1 а) нет; б) да; в) нет. № 2 б) 28 см. № 3 в) 90°. |
№ 1 а) да; б) да; в) нет. № 2 б) 12 см. № 3 б) 60°. |
III. Подведение итогов
Домашнее задание
П. 1-9, прорешать задачу из контрольной работы № 1 (поменяться вариантами).
Решение заданий контрольной работы № 1.
I уровень
Вариант I
№ 1. Дано: a ∩ b в точке О, а и с скрещивающиеся (рис. 1).
Могут ли прямые b и с быть параллельными?
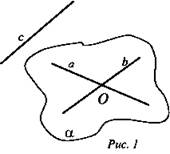
Решение:
1. Через а ∩ b в точке О проведем плоскость α (по теореме п. 3, стр. 7).
2. а и с - скрещивающиеся, значит, с ∉ α.
3. Прямые b и с могут быть параллельными. (Ответ: да.)
№ 2. Дано: ABCD - трапеция; α - плоскость; α ∩ АВ в точке М; α ∩ CD в точке N; AM = MB; CN = ND; MN = 8 см; AD = 10 см (рис. 2).
а) Доказать: AD || α.
б) Найти: ВС.
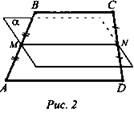
Доказательство: a) MN ∈ α; MN - средняя линия трапеции ABCD; MN || ВС и MN || AD no свойству средней линии. Значит, AD || α.
Решение: б) ![]() (Ответ: a) AD || α; б) ВС = 6 см.)
(Ответ: a) AD || α; б) ВС = 6 см.)
№ 3. Дано: ABCD - квадрат; МА - прямая; МА ∉ (ABCD) (рис. 3).
Доказать: МА и ВС - скрещивающиеся.
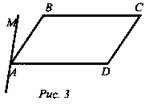
Найти: угол между прямыми МА и ВС, если ∠MAD = 45°.
Доказательство: ![]() в точке А ∉ ВС. Значит, МА и ВС - скрещивающиеся.
в точке А ∉ ВС. Значит, МА и ВС - скрещивающиеся.
Решение: ВС || AD - как противолежащие стороны квадрата, значит, угол между прямыми МА и ВС будет ∠MAD = 45° по условию. (Ответ: а) МА и ВС - скрещивающиеся; б) угол между прямыми МА и ВС равен 45°.)
Вариант II
№ 1. Дано: a ∩ b в точке О; а || с (рис. 4).
Могут ли прямые b и с быть скрещивающимися?
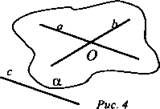
Решение:
1. Через a ∩ b в точке О проведем плоскость α (по теореме п. 3).
2. а || с - по условию, значит, если с ∈ α, то b ∩ с, а если с ∉ α, то b и с - скрещивающиеся. (Ответ: могут.)
№ 2. Дано: ABCD - трапеция, α - плоскость, α ∩ (ABCD) по прямой AD, то есть AD ∈ α, точка М - середина АВ, точка N - середина CD (рис. 5).
а) Доказать: MN || α.
б) Найти: AD, если ВС = 4 см, MN = 6 см.
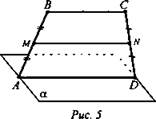
Доказательство: a) 1. MN - средняя линия трапеции ABCD, значит, MN || ВС и MN || AD. 2. Так как AD ∈ α по условию, то МN || α.
Решение: б) ![]() (Ответ: a) MN || α; б) AD = 8 см.)
(Ответ: a) MN || α; б) AD = 8 см.)
№ 3. Дано: ΔABC; CD - прямая; CD ∉ (ABC); точка Е - середина АВ, точка F - середина ВС (рис. 6).
а) Доказать: CD и EF - скрещивающиеся.
б) Найти: угол между прямыми CD и EF, если ∠DCА = 60°.
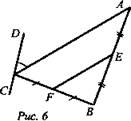
Доказательство: EF - средняя линия ΔABC, EF ∈ (ABC), CD ∉ (ABC), CD ∩ (ABC) в точке С, значит, CD и EF - скрещивающиеся прямые.
Решение: EF || СА - по свойству средней линии ΔАВС, значит, угол между прямыми CD и EF будет считаться угол между прямыми DC и СА, то есть ∠DCA, который равен 60°. (Ответ: a) CD и EF - скрещивающиеся; б) угол между прямыми СD и EF равен 60°.)
II уровень.
Вариант I
№ 1. Дано: α - плоскость, а || α, а ∉ α, b ∈ а (рис. 7).
Определите, могут ли прямые: а) быть параллельными; б) пересекаться; в) быть скрещивающимися.
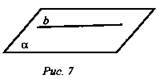
Решение:
а) ![]() значит, а и b могут быть параллельными;
значит, а и b могут быть параллельными;
б) ![]() значит, а и b не могут пересекаться;
значит, а и b не могут пересекаться;
в) ![]() значит, а и b могут быть скрещивающимися. (Ответ: а) да; б) нет; в) да.)
значит, а и b могут быть скрещивающимися. (Ответ: а) да; б) нет; в) да.)
№ 2. Дано: ABCD - трапеция, (AD || ВС); точка М ∉ (ABCD); QP - средняя линия трапеции; NK - средняя линия ΔAMD; EF - средняя линия ΔВМС; QP = 16 см; АD : ВС = 5 : 3 (рис. 8).
а) Доказать: EF || NK.
б) Найти: EF; NK.
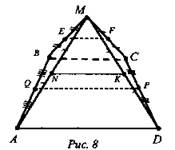
Доказательство:
1) EF || ВС и NK || AD - по свойству средней линии треугольника;
2) AD || ВС - по условию, значит EF || NK.
Решение: Пусть х - коэффициент пропорциональности k, тогда AD = 5х, ВС = 3х. Так как ![]() - по свойству средней линии трапеции, то составим и решим уравнение.
- по свойству средней линии трапеции, то составим и решим уравнение. ![]() значит, k = 4, тогда AD = 20 см, ВС = 12 см. Тогда
значит, k = 4, тогда AD = 20 см, ВС = 12 см. Тогда ![]()
![]() (Ответ: a) EF || NK; б) 10 см; 6 см.)
(Ответ: a) EF || NK; б) 10 см; 6 см.)
№ 3. Дано: ABCD - квадрат; КА ∉ (ABCD); КА ∩ (ABCD) в точке А. ∠AKB = 85°, ∠ABK = 45° (рис. 9).
а) Доказать: КА и CD - скрещивающиеся.
б) Найти: угол между прямыми КА и CD.
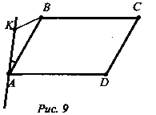
Доказательство: CD ∈ (ABCD), КА ∉ (ABCD) - по условию и КА ∩ (ABCD) в точке А ∉ CD, тогда КА и СD - скрещивающиеся.
Решение:
1) CD || АВ, CD = АВ, КА ∩ ВА в точке А, значит, углом между прямыми КА и CD будет являться ∠KАВ.
2) Так как ∠АКB = 85°, ∠АВК = 45°, то ∠КАВ = 180° - (∠АКB + ∠АВК) = 180° - (85° + 45°) = 50°. Ответ: а) КА и СD - скрещивающиеся; б) угол между прямыми КА и СD равен 50°.)
Вариант II
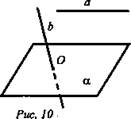
№ 1. Дано: α - плоскость, а || α, b ∩ α в точке О (рис. 10).
Определите, могут ли прямые а и Ь: а) быть параллельными; б) пересекаться; в) быть скрещивающимися.
Решение:
а) Так как а || α, b ∩ α в точке О, то а и b не могут быть параллельными;
б) b ∩ α в точке О; а || α, тогда а и b могут пересекаться;
в) а || α, b ∩ α в точке О, значит, а и b могут быть скрещивающимися. (Ответ: а) нет; б) да; в) да.)
№ 2. Дано: ΔABC, ΔKMNP - трапеция; КР || MN; EF - средняя линия ΔАВС и трапеции KMNP. КР : MN = 3 : 5, АС = 16 см (рис. 11).
а) Доказать: АС || КР.
б) Найти: КР и MN.
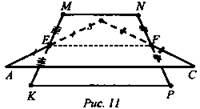
Доказательство: EF || АС - по свойству средней линии ΔАВС; EF || КР - по свойству средней трапеции KMNP. Значит, АС || КР.
Решение:
1. ![]()
2. Пусть k - коэффициент пропорциональности, тогда КР = 3k, MN = 5k.
![]() значит,
значит, ![]() (Ответ: а) АС || КР; б) КР = 6 см; MN = 10 см.)
(Ответ: а) АС || КР; б) КР = 6 см; MN = 10 см.)
№ 3. Дано: ABCD - ромб; точка М ∉ (ABCD); МС - прямая; МС ∩ (ABCD) в точке С (рис. 12).
а) Доказать: МС и AD - скрещивающиеся.
б) Найти: угол между МС и AD, если ∠MBC = 70°, ∠BMC = 65°.
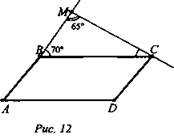
Доказательство: МС ∉ (ABCD), MС ∩ (ABCD) в точке AD ∈ (ABCD), значит, МС и AD - скрещивающиеся прямые.
Решение:
1. AD || ВС - как противолежащие стороны ромба; ВС ∩ МС в точке С, значит, утлом между прямыми МС и AD будет считаться ∠MCB.
2. ![]() (Ответ: а) МС и AD - скрещивающиеся; б) угол между МС и AD равен 45°.)
(Ответ: а) МС и AD - скрещивающиеся; б) угол между МС и AD равен 45°.)
III уровень
Вариант I
№ 1. Дано: α и β - плоскость, α ∩ β по прямой l, а || l; а и b - скрещивающиеся (рис. 13.).
Определите, могут ли прямые а и b; а) лежать в одной плоскости; б) лежать в разных плоскостях α и β; в) пересекать плоскости α и β.
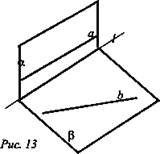
Решение:
а) Так как а и b - скрещивающиеся, то они лежат в разных плоскостях; не могут лежать в одной плоскости.
б) Так как а и b - скрещивающиеся, то они могут лежать только в разных плоскостях.
в) Если прямая а ∩ α, то а ∩ l - что противоречит условию а || l, если прямая а ∩ β, то а ∩ l - что противоречит условию а || l; прямая b может пересекать плоскость α, не пересекает плоскость β. (Ответ: а) нет; б) да; в) нет.)
№ 2. Дано: ΔАВС; α - плоскость; α ∩ (ABC) по прямой MN; М ∈ АВ; N ∈ ВС; АМ : МВ = 3 : 4; CN : BC =3 : 7; MN = 16 см (рис. 14).
а) Доказать: АС || α.
б) Найти: АС.
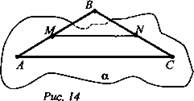
Доказательство: Рассмотрим ΔABC и ΔMBN. У них: a) ∠B - общий; б) ![]() Значит, ΔABC ~ ΔMBN ⇒ ∠BMN = ∠BAC и ∠BNM = ∠BCA - и они соответственные при прямых MN и AC; AB и ВС - секущие, значит, MN || AC.
Значит, ΔABC ~ ΔMBN ⇒ ∠BMN = ∠BAC и ∠BNM = ∠BCA - и они соответственные при прямых MN и AC; AB и ВС - секущие, значит, MN || AC. ![]()
Решение:
Из ΔАВС ~ ΔMBN ⇒ ![]() (Ответ: а) АС || α; б) АС = 28 см.)
(Ответ: а) АС || α; б) АС = 28 см.)
№ 3. Дано: А, В, С и D - не лежат в одной плоскости. АС = 6 см; BD = 8 см. Расстояние между серединами отрезков AD и ВС равно 5 см (рис. 15).
Найти: угол между прямыми АС и BD.
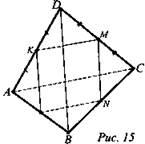
Решение:
1. Отметим точку К - середину AD, N - середину ВС. Проведем КМ || BD, тогда углом между прямыми АС и BD будем считать ∠KMN.
2. КМ = 1/2АС = 3 см; MN = 1/2BD = 4 см; KN = 5 см (как расстояние между прямыми AD и ВС).
3. Получили ΔKMN со сторонами 3 см, 4 см, 5 см - это египетский треугольник. Значит, ∠КMN = 90°. (Ответ: 90°.)
Вариант II
№ 1. Дано: α и β по прямой l; l ∩ а в точке А, l || b (рис. 16).
Определите, могут ли прямые а и b: а) лежать в одной из данных плоскостей; б) лежать в разных плоскостях α и β; в) пересекать плоскости α и β.
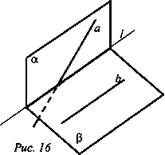
Решение:
а) b || l, значит, b || α и b || β; а ∩ l, значит, а может пересекать либо α и лежать в β, либо пересекать β и лежать в α. Поэтому а и b могут лежать в одной из данных плоскостей;
б) а и b могут лежать в разных плоскостях α и β;
в) b || l ⇒ b не может пересекать ни α, ни β. А прямая а ∩ l, поэтому может пересекать либо α, либо β. (Ответ: а) да; б) да; в) нет.)
№ 2 Дано: ΔАВС; α - плоскость; AC ∈ α; l - прямая АВ ∩ l в точке М; ВС ∩ l в точке N; BN : NC= 2 : 3, АМ : АВ = 3 : 5; AС = 30см (рис. 17).
а) Доказать: MN || α.
б) Найти: MN.
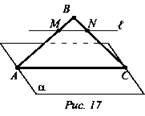
Доказательство: Рассмотрим ΔMBN и ΔAВС. У них: а) ∠В - общий; б) ![]() Значит, ΔMBN ~ ΔАВС. Из этого следует, что ∠BMN = ∠BAC и ∠BNM = ∠BCA - они являются соответственными при прямых MN и АС и секущих АВ и ВС. Значит,
Значит, ΔMBN ~ ΔАВС. Из этого следует, что ∠BMN = ∠BAC и ∠BNM = ∠BCA - они являются соответственными при прямых MN и АС и секущих АВ и ВС. Значит, ![]()
Решение: Из ![]() (Ответ: a) MN || α; б) MN = 12 см.)
(Ответ: a) MN || α; б) MN = 12 см.)
№ 3. Дано: А, В, С, D - не лежат в одной плоскости. АВ = CD = 6 см. Расстояние между серединами отрезков АВ и ВС = 3 см (рис. 18).
Найти: угол между прямыми АВ и CD.
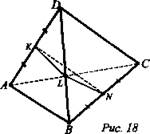
Решение:
1. Отметим точку К - середину AD и точку N середину ВС. Проведем KL || АВ; LN || DC, тогда углом между прямыми АВ и CD будем считать ∠KLN.
2. KL || АВ и ![]()
![]() как расстояние между серединами отрезков AD и ВС.
как расстояние между серединами отрезков AD и ВС.
3. Получим ΔKLM - равносторонний, значит, ∠KLN = 60°. (Ответ: 60°.)