Поурочные разработки по геометрии 10 класс
Параллельные плоскости - ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие параллельных плоскостей;
2) доказать признак параллельности двух плоскостей;
3) сформировать у учащихся навыки применения этого признака при решении задач.
Ход урока
I. Организационный момент
Сообщить тему урока и сформулировать цели урока.
II. Актуализация знаний учащихся
Анализ контрольной работы.
1. Подвести итоги контрольной работы.
2. Анализ ошибок, допущенных в работах.
Подготовка учащихся к восприятию нового материал.
- Сформулировать А3.
- Сформулировать утверждение 1° п. 6.
- Признаки подобия треугольников.
- Теорема об отношениях площадей подобных треугольников.
- Свойство средней линии треугольника.
![]()
III. Изучение нового материала
1. Определение параллельных плоскостей.
2. По аксиоме 3 плоскости пересекаются по прямой. Но возможен еще один случай взаимного расположения двух плоскостей, если они не имеют общей точки.
На доске схема

В тетрадях учащихся и на доске рисунки и записи.
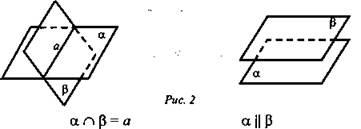
3. Признак параллельности плоскостей.
Дано: ![]()
![]() (рис. 3).
(рис. 3).
Доказать: α || β.
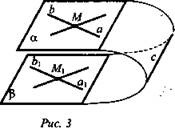
Доказательство: От противного. Пусть α ∩ β = с,
1) Тогда ![]() значит, а || с (по утверждению 1 ° п. 6).
значит, а || с (по утверждению 1 ° п. 6).
2) ![]() значит, b || с.
значит, b || с.
3) Имеем а || b, то есть через точку М проходят две прямые а и b, параллельные прямой с. Получили противоречие. Значит, α || β.
IV. Закрепление изученного материала
№ 51. (еще один признак параллельности плоскостей).
Дано: ![]() (рис. 4).
(рис. 4).
Доказать: α || β.
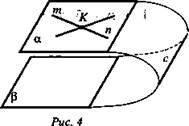
Доказательство: Допустим, что α и β не параллельны. Тогда они пересекаются по некоторой прямой с. Так как m || β, n || β, то по утверждению 1° m || с, n || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по теореме о параллельных прямых. Получили противоречие. Значит, α || β.
№ 53. Дано: отрезки A1A2, В1В2, C1C2 не лежат в одной плоскости и имеет общую середину - точку О (рис. 5).
Доказать: А1В1С1 || A2В2С2.
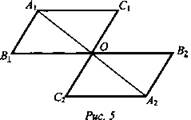
Доказательство:
1) А1А2 и В1В2 лежат в одной плоскости по следствию из A1 (через две пересекающиеся прямые проходит плоскость, и притом только одна). А1В1А2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А1В1 || А2В2.
2) Аналогично A1A2 и С1С2 лежат в одной плоскости. A1C1A2C2 - параллелограмм. Отсюда, A1С1 || А2С2.
3) ![]()
По признаку параллельности плоскостей А1В1С1 || A2В2С2.
№ 54. Дано: ΔADC. В ∉ ADC. М, N, Р - середины В А, ВС, BD соответственно. SADC = 48 см2 (рис. 6).
Доказать: a) MPN || ADC. б) Найти: SMNP.
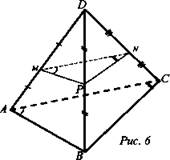
Решение:
а) В ΔABD: МР - средняя линия, МР || AD. В ΔBCD: PN - средняя линия PN || DC. МР ∩ PN = Р, AD ∩ DC = D. По признаку параллельности двух плоскостей (MNP) || (ADC). Что и требовалось доказать.
б) ∠NMP = ∠CAD, ∠MNP = ∠ACD как углы с сонаправленными сторонами, поэтому ΔMPN ~ ΔADC по двум углам. ![]() (по теореме об отношениях площадей подобных треугольников).
(по теореме об отношениях площадей подобных треугольников). ![]() (по свойству средней линии треугольника)
(по свойству средней линии треугольника) ![]()
![]() (Ответ: 12 см2.)
(Ответ: 12 см2.)
V. Подведение итогов (в форме текста)
1. Могут ли прямая и плоскость не иметь общих точек?
2. Верно ли, что если две прямые не пересекаются, то они параллельны?
3. Плоскости α и β параллельны, прямая т лежит в плоскости α. Верно ли, что прямая m параллельна плоскости β?
4. Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет только одну общую точку?
5. Боковые стороны трапеции параллельны плоскости α и плоскости трапеции?
6. Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
7. Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?
8. Верно ли, что любые четыре точки лежат в одной плоскости?
9. Верно ли, что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельна плоскости α?
№ вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Ответ |
да |
нет |
да |
нет |
да |
нет |
нет |
нет |
да |
Домашнее задание
П. 10, № 55, 56, 57.
Задача 56
Дано: ![]() (рис. 7).
(рис. 7).
Доказать: а ⊂ α.
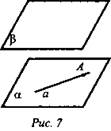
Решение: Мы знаем, что если некоторая прямая а пересекает плоскость α, то она пересекает также любую плоскость, параллельную α. Если а не параллельна β, то она пересекает β, а значит, и плоскость α, а по условию а || β. Значит, а не может пересекать плоскость α и, так как она имеет с плоскостью α общую точку А, то а ⊂ α.
Задача 55
Записать в тетрадь и разобрать решение задачи, приведенное в учебнике.
Задача 57
Дано: α || β, а || α.
Доказать: а || β или а ⊂ β.
Решение: Пусть а не параллельна β, тогда она пересекает β, а значит, пересекает α (задача 55 решена в учебнике). Значит, предположение неверно, то есть или а || β или а ⊂ β.