Поурочные разработки по геометрии 10 класс
Повторение теории, решение задач на вычисление площади поверхности призмы - ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА - МНОГОГРАННИКИ
Цели урока:
1) повторить определения призмы, ее элементов, вывод формулы площади боковой поверхности призмы;
2) продолжить формирование навыков решения задач;
3) обеспечить в ходе урока воспитание трудолюбия, самостоятельности в поисках и выборе пути решения;
4) развивать творческие способности учащихся, познавательную активность.
Ход урока
I. Организационный момент
Постановка целей и задач урока.
II. Проверка домашнего задания
Проверить решение домашних задач № 231 и № 232 - дать задание двум ученикам подготовить на доске краткое решение задачи, ход решения заслушать. Учащимся дается задание: внимательно выслушать решение и быть готовым ответить на вопрос: «Верно ли решена задача? Какие замечания к решению есть у тебя?».
Задача № 231
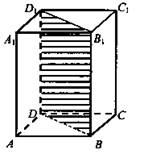
Решение: ![]()
1) Пусть АВ = 15 см; AD = 8 см; ∠DAB = 60°.
2) Отрезок DB - меньшая диагональ параллелограмма ABCD, найдем DB по теореме косинусов DB2 ![]()
![]()
3) По условию, параллелепипед ABCDA1B1C1D1 - прямой, диагональное сечение DBB1D - прямоугольник, площадь которого 130 см2. Следовательно, зная одну из сторон прямоугольника DB = 13 см, находим вторую сторону ВВ1 - высоту данного прямого параллелепипеда. ВВ1 = 130 : 13 = 10 (см).
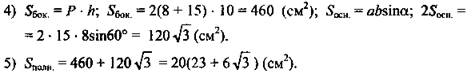
(Ответ: ![]() )
)
Задача № 232
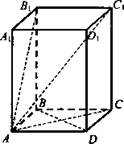
Решение: Рассмотрим параллелепипед ABCDA1B1C1D1. ∠C1AB1 - угол между диагональю и боковой гранью. ∠С1АС - угол между диагональю и основанием, тогда ![]()
![]() Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений ![]()
![]() Площадь боковой поверхности равна
Площадь боковой поверхности равна ![]()
![]() (Ответ:
(Ответ: ![]() )
)
III. Актуализация знаний учащихся
1) Фронтальная работа. Работа проводится с целью повторения теоретического материала двух предыдущих уроков. На уроке по данной теме можно использовать справочную таблицу «Призма».
Таблица
Призма
1) n-угольники ABCDE, A1B1C1D1E1 равны |
(АА ⊥ AВС) ⇔ (прямая призма) |
2) n = параллелограммов АВВ1А1,..., ЕАА1Е1 |
|
|
|
(OO1 ⊥ АВС), (OO1 ⊥ A1B1C1) ⇔ OO1 - высота призмы (АА1 - наклонная к плоскости AВС) ⇔ (наклонная призма) |
(прямая призма, основание - правильный многоугольник) ⇔ (правильная призма. |
![]() Свойства прямой призмы: 1. Боковые грани - прямоугольники. 2.
Свойства прямой призмы: 1. Боковые грани - прямоугольники. 2. ![]() P — периметр основания; h - высота призмы.
P — периметр основания; h - высота призмы.
Вопросы классу:
1. Укажите на таблице высоту призмы, диагональ призмы, диагональ грани призмы.
2. Сколько вершин, ребер, граней имеет шестиугольная призма?
3. Какое наименьшее число ребер, граней, вершин может иметь призма?
4. Как называется призма, у которой каждая грань может служить основанием?
5. Сколько диагоналей можно провести в четырехугольной призме; в треугольной призме?
6. Докажите, что все высоты призмы равны.
7. Докажите, что любое ребро основания прямой призмы перпендикулярно к любому боковому ребру.
8. Какой отрезок служит проекцией диагонали прямой призмы на плоскость основания? На плоскость боковой грани?
9. Определите вид призмы, если две ее боковые грани, имеющие общее ребро, являются прямоугольниками.
10. Может ли быть наклонной призма, основание которой — прямоугольник?
11. Может ли быть наклонной призма, две боковые грани которой - прямоугольники?
12. Все боковые грани призмы - квадраты. Является ли эта призма правильной, если ее основание - треугольник, четырехугольник?
13. Чему равны градусные меры двухгранных углов, образованных боковыми гранями правильной призмы, если эта призма:
а) треугольная;
б) четырехугольная;
в) пятиугольная.
14. Докажите теорему о площади боковой поверхности прямой призмы. Можно использовать таблицу.
15. Измерения прямоугольного параллелепипеда равны 1 м, 2 м, 3 м. Найдите площадь его полной поверхности. Найдите площадь его боковой поверхности, если боковые ребра:
а) больше ребер основания:
б) меньше ребер основания.
2) Индивидуальная работа
I уровень
Карточка № 1
Прочитайте условие задачи и разберите ее решение.
В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6 см, и углом при вершине 120°. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10 см. Найдите площадь боковой поверхности.
Дано: АВСА1В1С1 - прямая призма; ΔАВС - равнобедренный; ∠ABC = 120°; АС = 6 см, АС = 10 см.
Найти: Sб.п..
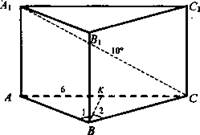
Решение:
1. В плоскости α = (А, В, С) рассмотрим ΔАВС. Проведем ВК ⊥ АС.
2. АК = КС; ∠1 = ∠2 (свойство высоты равнобедренного треугольника).
3. Рассмотрим ΔАКВ - прямоугольный; ![]()
![]()
4. Рассмотрим ΔАА1С - прямоугольный, ![]() (по теореме Пифагора),
(по теореме Пифагора), ![]()
5. ![]() (Ответ:
(Ответ: ![]() )
)
II уровень
Карточка № 2
Прочитайте условие задачи и приведите в приведенном решении нужные обоснования.
В правильной четырехугольный призме диагональ, равная 6 см, образует с плоскостью основания угол, равный 30°. Найдите высоту призмы и ее объем.
Дано: ABCDA1B1C1D1 - правильная призма; B1D = 6 см; ∠(B1D, α) = 30°.
Найдите: а) В1В; б) Vпр.
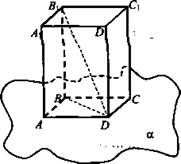
Решение:
1. BD = прαВ1D ⇒ ∠B1DB - угол между диагональю B1D и плоскостью основания (по определению). ∠B1DB = 30°.
2. ΔB1DB - прямоугольный, так как ...
3. В1В - катет, лежащий против угла 30°. В1В = 1/2B1D, так как ...
4. BD = B1D · cos30°, так как ...
5. ABCD - квадрат, так как ...
6. ΔABD - равнобедренный и прямоугольный, ВD2 = 2AD2, так как ...
![]()
7. ![]() (Ответ: ВВ1 = 3 см; Vпр. = 40,5 см3.)
(Ответ: ВВ1 = 3 см; Vпр. = 40,5 см3.)
III уровень
Карточка № 3
В основании прямой призмы лежит прямоугольный треугольник ABC (∠C - прямой) с острым углом а и гипотенузой с. Найдите угол, образованный плоскостью нижнего основания призмы и плоскостью, проходящей через катет АС и вершину В1 верхнего основания, если высота призмы равна Н.
Дано: АВСА1В1С1 - прямая призма АВ = с; ВВ1 = Н; ∠A = а.
Найдите: ∠(γ, (AC, B1).
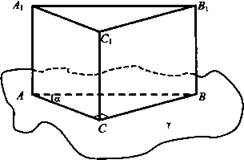
План.
1. Постройте сечение, проходящее через АС и В1. Плоскость сечения обозначьте β. 2. Постройте линейный угол между плоскостями β и γ. Помните, что АС ⊥ BС. 3. Найдите катет ВС. 4. Найдите тангенс построенного линейного угла. 5. Запишите искомый угол.
Ответ:
IV. Решение задач
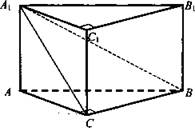
1). № 235. Дано: АВСА1В1С1 - прямая призма; ∠ABC = 90°; ∠CAB = φ; ΔА1СВ - сечение; ∠ACBA1 = Q.
Найти: ![]()
Решение:
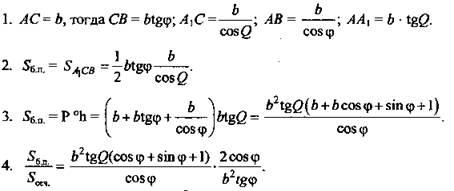
(Ответ: ![]() )
)
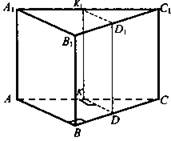
Задача 234
Дано: ABCA1B1C1 - прямая призма; ![]()
![]()
Найти: ![]()
Решение:
1. AC = 29 см; AK = 14,5 см. ΔABC ~ ΔDKC (по двум углам); ![]()
2. ![]() (Ответ: 580 см2.)
(Ответ: 580 см2.)
V. Подведение итогов урока
1) Обучающая самостоятельная работа
I уровень
В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник АСВ (∠C = 90°); АС = 4; ВС = 3. Через сторону АС и вершину В1 проведена плоскость. ∠B1AC= 60°. Найдите площадь боковой поверхности призмы.
II уровень
В основании прямой призмы ABCA1B1C1 лежит прямоугольный ΔАВС (∠C = 90°). Через сторону ВС и вершину A1 проведена плоскость, ∠BA1C = 30°, А1В = 10; АС = 5. Найдите площадь боковой поверхности призмы.
III уровень
1) В прямом параллелепипеде ABCDA1B1C1D1 АВ = 1; ВС = 7√3; ∠ABC = 150°. Через диагональ АС и вершину В1 проведена плоскость, составляющая с плоскостью основания угол 60°. Найдите площадь боковой поверхности параллелепипеда.
2) Оценить работу учащихся на уроке.
Домашнее задание
1) П. 25-27, вопросы к главе III 1-9. 2) Решить задачи: I уровень № 236, 238. II уровень № 236, 238, 298.
Решения задач самостоятельной работы
I уровень
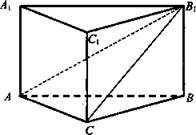
Решение:
1. ![]()
![]() ΔАСВ1 - прямоугольный.
ΔАСВ1 - прямоугольный.
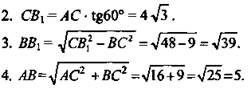
![]() (Ответ:
(Ответ: ![]() )
)
II уровень
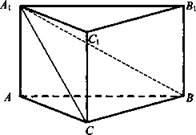
Решение:
1. A1C ⊥ BC (по теореме о трех перпендикулярах)
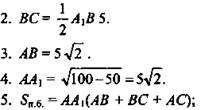
![]() (Ответ:
(Ответ: ![]() )
)
III уровень
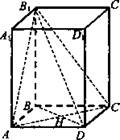
Решение:
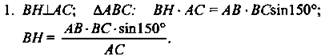
2. ΔАВС: по теореме косинусов ![]()
![]()
![]()
![]()
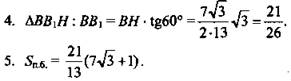
(Ответ: ![]() )
)