Поурочные разработки по геометрии 10 класс
Решение задач на вычисление площади поверхности призмы - ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА - МНОГОГРАННИКИ
Цели урока:
1) продолжить формирование навыков решения задач по теме;
2) проверить навыки решения основных типов задач;
3) обеспечить в ходе урока воспитание целеустремленности, настойчивости, самостоятельности в поисках и выборе пути решения задач;
4) развивать творческие способности учащихся, их познавательную активность.
Ход урока
I. Организационная часть
Постановка целей и задач урока.
II. Проверка домашнего задания
№ 236 проверяется по готовому слайду кодоскопа.
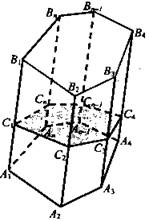
Решение: Пусть ![]() перпендикулярное сечение наклонной призмы
перпендикулярное сечение наклонной призмы ![]()
![]() Тогда площадь грани А1В1В2А2 равна
Тогда площадь грани А1В1В2А2 равна ![]() так как боковая грань - это параллелограмм, а СС1 - высота этого параллелограмма. Сложив площади всех боковых граней, получим
так как боковая грань - это параллелограмм, а СС1 - высота этого параллелограмма. Сложив площади всех боковых граней, получим ![]()
![]() где l - длина бокового ребра; Рсеч. - периметр перпендикулярного сечения.
где l - длина бокового ребра; Рсеч. - периметр перпендикулярного сечения.
Двоим учащимся дается задание подготовить краткую запись решения задач № 238 и 298, ход решения заслушать.
№ 238
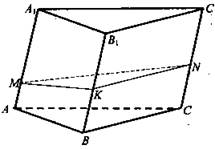
Решение: По условию BB1 = 24 см, грани AA1B1В и ВВ1С1С взаимно перпендикулярны; ΔMNK прямоугольный, ![]() Найдем периметры перпендикулярного сечения MNK.
Найдем периметры перпендикулярного сечения MNK. ![]()
![]() (Ответ: 2016 см2.)
(Ответ: 2016 см2.)
№ 298
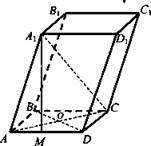
Решение:
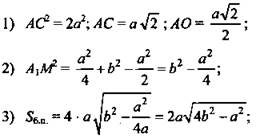
![]() (Ответ:
(Ответ: ![]() )
)
III. Актуализация знаний
Подготовка к проверочной самостоятельной работе.
1. Устное решение задач планиметрии по готовым чертежам.
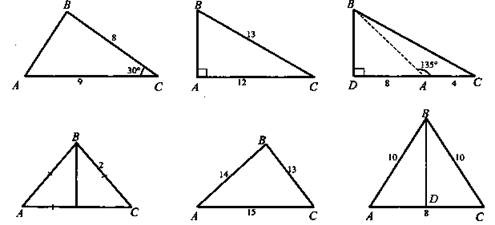
Найти площадь ΔАВС.
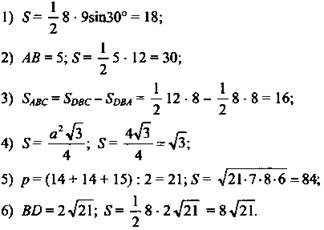
2. Письменное решение планиметрической задачи, краткий ход решения ученик записывает на доске.
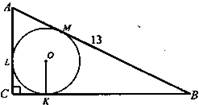
Решение:
1) КВ = х; ВМ = х; АМ = 13 - х; АL = 13 - х.
2) КС = СК = 2.
(Ответ: SABC = 18 см2.)
3. Применение знаний в стандартной ситуации
Задача (ученик решает у доски).
Основанием прямой призмы является прямоугольный треугольник, гипотенуза которого равна m, а острый угол равен 60°. Через катет, противоположный этому углу, и противоположную этому катету вершину другого основания проведено сечение, составляющее угол 45° с плоскостью основания.
1. Докажите, что ΔА1СВ прямоугольный.
2. Укажите различные способы вычисления площадей основания и сечения призмы.
3. Вычислите площадь основания призмы.
4. Вычислите площадь боковой поверхности призмы.
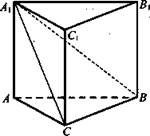
Решение:
1) АС ⊥ СВ; AA1 ⊥ CB1, значит, АС ⊥ СВ; ΔА1СВ - прямоугольный.
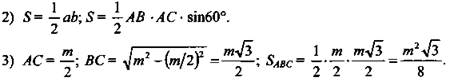
4) ΔАА1С - равнобедренный и прямоугольный, ![]()
5) ![]() (Ответ:
(Ответ: ![]() )
)
IV. Самостоятельная работа проверочного характера
I уровень
Вариант I
1. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы - ромб со стороной 5 см и тупым углом 120°. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
Вариант II
1. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы - ромб с острым углом 60°. Боковое ребро призмы равно 10 см, а площадь боковой поверхности - 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
II уровень
Вариант I
1. Основание прямой призмы - прямоугольный треугольник с катетами 15 и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
2. Боковая поверхность правильной четырехугольной призмы имеет площадь 16 дм2. Диагональ основания призмы равна 4√2 дм. Найдите площадь сечения призмы, проходящего через диагонали двух смежных боковых граней, имеющих общую вершину.
Вариант II
1. Основание прямой призмы - прямоугольный треугольник с гипотенузой 25 см и катетом 20 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
2. Высота правильной четырехугольной призмы равна 1 дм, а площадь боковой поверхности равна 16 дм2. Найдите площадь сечения призмы, проходящего через диагональ нижнего основания, и противолежащую вершину верхнего основания.
III уровень
Вариант I
1. Основание прямой призмы - равнобедренный треугольник с боковой стороной 6 см и углом при вершине 120°. Диагональ наибольшей боковой грани образует с плоскостью основания призмы угол 60°. Найдите площадь боковой грани и полной поверхности призмы.
2. Площадь боковой поверхности правильной четырехугольной призмы равна Q. Сечение призмы, проходящее через диагональ нижнего основания и противолежащую вершину верхнего основания, образует с плоскостью основания призмы угол α. Найдите площадь сечения.
Вариант II
1. Основание прямой призмы - равнобедренный треугольник с основанием 6√3 см и углом при основании 30°. Диагональ меньшей боковой грани образует с плоскостью основания призмы угол 45°. Найдите площадь боковой и полной поверхности призмы.
2. Сечение призмы, проходящее через середину бокового ребра и диагональ основания, не пересекающую данное ребро, образует с плоскостью основания угол α. Найдите площадь сечения.
Решения задач самостоятельной работы
I уровень
Вариант I
1. Решение:
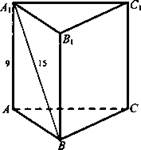
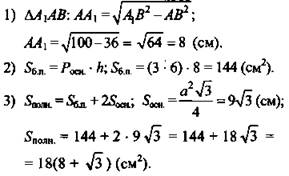
(Ответ: ![]() )
)
2. Решение:
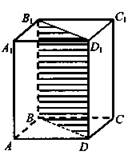
1) ∠ABC= 120°; ∠BAD = 60°; ΔABD - равносторонний; BD = 5 см.
(Ответ: Scеч. = 60 см2 .)
Вариант II
1. Решение:
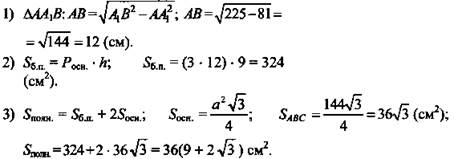
(Ответ: ![]() )
)
2. Решение:
1) ![]() По условию,
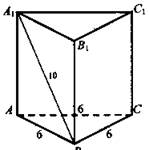
По условию, ![]() h = BB1 = 10 см, значит, Росн. = 240 : 10 = 24 (см).
h = BB1 = 10 см, значит, Росн. = 240 : 10 = 24 (см).
2) АВ = Р : 4 = 24 : 4 = 6 (см).
3) ∠BAD = 60°; ΔABD - равносторонний; BD = 6 см.
4) ![]() (Ответ: Sсеч. = 60 см..
(Ответ: Sсеч. = 60 см..
II уровень
Вариант I
1. Решение:
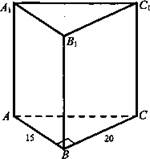
![]() (Ответ: 360 см2; 660 см2.)
(Ответ: 360 см2; 660 см2.)
2. Решение:
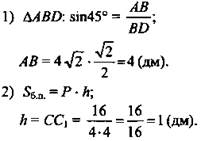
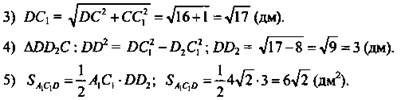
(Ответ: ![]() )
)
Вариант II
1. Решение:
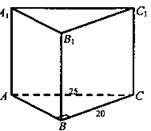
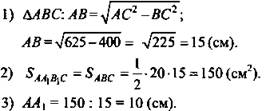
![]()
(Ответ: 600 см2; 900 см2.)
2. Решение:
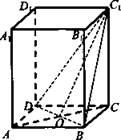
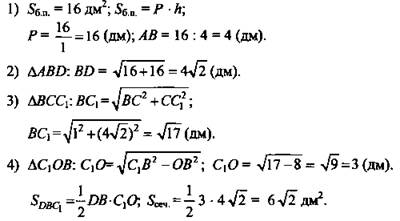
(Ответ: ![]() )
)
III уровень
Вариант I
1. Решение:
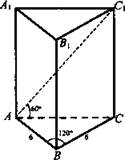
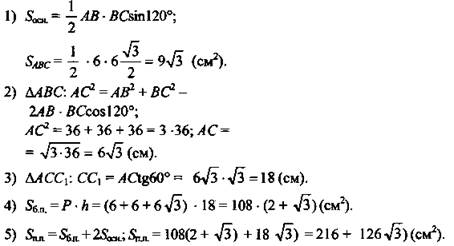
(Ответ: ![]() )
)
2. Решение:
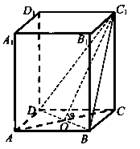
1) ![]()
2) DB ⊥ OC, то DB ⊥ OC, по теореме о трех перпендикулярах, ⇒ ∠C1OC - линейный угол двугранного угла C1DBC. По условию, ∠C1OC = α.
3) Пусть ![]()
4) ΔADB: ![]()
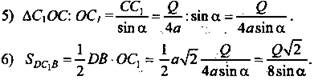
(Ответ: ![]() )
)
Вариант II
1. Решение:
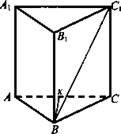
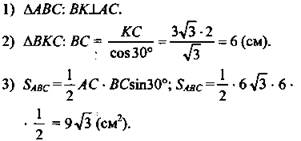
4) Меньшая боковая грань та, что содержит меньшее основание ∠C1BC = 45°, ΔВС1С - равнобедренный, значит, СС1 = 6 см.
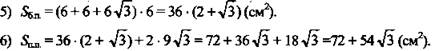
(Ответ: ![]() )
)
2. Решение:
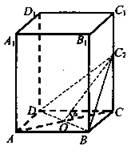
1) ![]()
2) DB ⊥ OC, то DB ⊥ OC2, по теореме о трех перпендикулярах, ⇒ ∠C2OC - линейный угол двугранного угла C2DBC, ∠C2OC = α.
3) Пусть АВ = а, ![]()
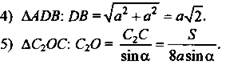
![]() (Ответ:
(Ответ: ![]() )
)
V. Подведение итогов
Домашнее задание
1. Повторить п. 25, 26.
2. Решить задачи другого варианта самостоятельной работы своего уровня.