Контрольная работа № 5.2 по теме «Скалярное произведение векторов в пространстве. Движения» - Движения - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цель урока:

- проверить знания, умения и навыки учащихся по теме «Скалярное произведение векторов в пространстве. Движения».

Ход урока

I. Организационный момент

Сообщить тему урока, сформулировать цель урока, нормы оценки данной работы и основные требования к оформлению решения задач.

II. Выполнение контрольной работы

Текст контрольной работы раздать учащимся в распечатанном виде (см. приложение).

III. Подведение итогов

Домашнее задание

1. Решить задачи, с которыми не справился ученик во время контрольной работы. В конце урока (после окончания работы) можно вывесить ответы и указания к решению задач, вошедших в контрольную работу (условия задач контрольной работы в распечатанном виде выдаются учащимся на дом).

2. Повторить теорию главы V «Метод координат в пространстве».

§ 1-3, с. 100-120 (п. 42-49).

Решение задач вошедших в контрольную работу № 5.2.

I уровень

Вариант I

1. Дано:

Найти: а) ; б) значение m, при котором .

Решение:

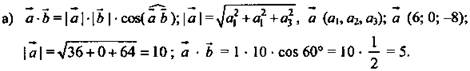
если так как то 24 – 8m = 0, m = 3.

(Ответ: а) = 5; б) m = 3.)

2. Дано: А(3; -1; 3); С(2; 2; 3); В(3; -2; 2); D(1; 2; 2).

Найти: угол между прямыми АВ и CD.

Решение: Рассмотрим направляющие векторы прямых АВ и CD. Найдем координаты Для нахождения угла J между прямыми АВ и CD воспользуемся формулой где {x1; y1; z1} -координаты вектора {x2; y2; z2} - координаты cos φ = 1/2, следовательно J = 60°. (Ответ: 60°.)

3. Дано: DABC - правильный тетраэдр, АВ = a, D → D1 при симметрии относительно плоскости AВС (рис. 1).

Найти: DD1.

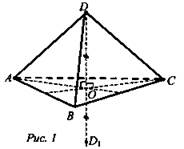
Решение:

1. DO ⊥ (ABC). O ∈ (ABC) ⇒ 10 → 0. D → D2: OD = OD1 (симметрия относительно плоскости является движением, т.е. сохраняет расстояние между точками) DD1 = 2OD.

2. Найдем длину DO из ΔDOC: ∠DOC = 90°; DC = а (по условию); точка О — центр описанной около ΔAВС окружности ⇒ (Ответ: .)

Вариант II

1. Дано:

Найдите: а) ; б) значение m, при котором

Решение:

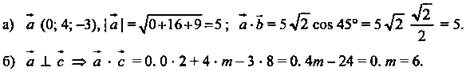
(Ответ: а) 5; б) m = 6.)

2. Дано: A(1; 1; 2), B(0; 1; 1), С(2; -2; 2), D(2; -3; 1).

Найти: угол между прямыми АВ и CD.

Решение: Аналогично заданию 2 (Вариант № 1) имеем: (-1; 0; -1); (0; -1 ;-1). (Ответ: 60°.)

3. Дано: DABC - правильный тетраэдр, АВ = a, (ABC) → (A1B1C1) при симметрии относительно точки D (рис. 2).

Найти: расстояние между плоскостями ABC и А1В1С1.

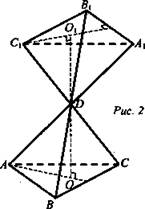
Решение:

1. Симметрия относительно точки является движением, следовательно сохраняет расстояние между соответствующими точками. Более того (ABC) || (A1B1C1), ΔАВС = ΔА1В1С1, a DO = DO1. 2DO = ОО1.

2. Аналогичные вычисления (№ 3 Вариант № 1) приводят к аналогичному результату.

(Ответ: .)

II уровень

Вариант I

1. Дано:

Найти:

Решение: так как по условию так как Подставим значения скалярных произведений векторов в (Ответ: -1.)

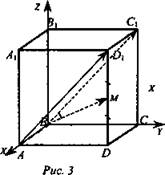
2. Дано: ABCDA1B1C1D1 - куб, DM = MD1 (рис. 3).

Найти: угол между прямыми AD1 и ВМ.

Решение:

1. Введем систему координат Bxyz.

2. Рассмотрим направляющие векторы прямых AD1 и ВМ. следовательно Для нахождения угла между прямыми воспользуемся формулой где (x1, y1, z1), (x2, y2, z2). Пусть ребро куба АВ = а, тогда В(0; 0; 0); С1(0; а; а); М(а; а; a/2); (0; а; а); (а; а; a/2). (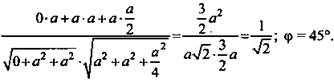Ответ: 45°.)

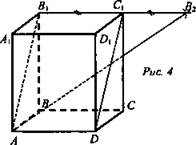
3. Дано: ABCDA1B1C1D1 - куб, АВ = а, В1 → В2 при симметрии относительно плоскости CC1D1 (рис. 4).

Найдите: АВ2.

Решение.

1. Построим точку В2: B1 → В2; В1С1 ⊥ C1D; С1В1 = С1B2.

2. Рассмотрим ΔAB1B2: ∠AB1B2 = 90° (так как B1B2 ⊥ A1B1C1; B1B2 ⊥ AB1). АВ1 = а√2; B1B2 = 2a. (Ответ: a√6..

Вариант II

1. Дано:

Найти:

Решение: так как

(Ответ: 11.)

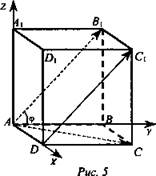
2. Дано: ABCDA1B1C1D1 - куб (рис. 5).

Найти: угол между прямыми АС и DC1.

Решение:

1. Введем систему координат Axyz.

2. Направляющие векторы прямых АС и DC. Используя формулу cos φ (приведенную в решении задач варианта 1) найдем φ. следовательно Пусть АВ = а, тогда А(0; 0; 0); (0; а; а2); (а; а; 0); (Ответ: 60°.)

3. Дано: ABCDA1B1C1D1 — куб, АВ = a, D → D2 при симметрии относительно прямой B1D1 (рис. 6).

Найдите: BD2.

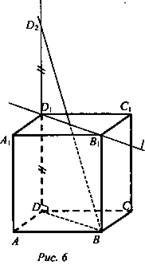
Решение:

1. DD1 ⊥ A1D1C1. DD1 = D1D2 (по определению симметрии относительно прямой).

2. ΔDD2B - прямоугольный; DD2 = 2а; DB = а√2 . (Ответ: a√6.)

III уровень

Вариант I

1. Дано:

Найдите:

Решение:

(Ответ: 6.)

2. Дано: DABC - пирамида; DA ⊥ DB ⊥ DC; DA = DB = DC = а (рис. 7).

Найдите: угол между плоскостями DAB и ABC.

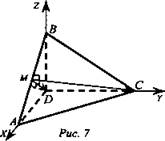
Решение:

1) АС = AD = DC, ΔАВС - правильный.

2) Угол между плоскостями измеряется величиной двугранного угла. МС ⊥ АВ ⇒ DM ⊥ АВ (теорема о трех перпендикулярах). ∠CMD - угол между плоскостями DAB и ABC.

3) D(0; 0; 0), A(a; 0; 0), B(0; a; 0), С(0; а; 0), M(a/2; 0; a/2). (-a/2; а; -a/2) : (-a/2; а; -a/2).

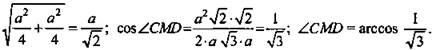
3. Дано: a; α; a || α; при движении a → a1, α → α1 (рис. 8).

Доказать: a1 || α1

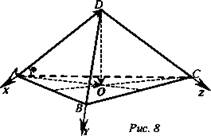
Если по условию a || α, то все точки прямой находятся на одинаковом расстоянии от α.

Предположим, что при движении a1 не|| α1 значит, a1 ∩ α1 = М, так как точки прямой а1 находятся на различных расстояниях от плоскости α1, а это противоречит тому, что при движении расстояние между точками сохраняется. Значит, предположение неверное, т. е. a1 || α1, что и требовалось доказать.

Вариант II

1. Дано:

Найти:

Решение: (Ответ: √109.)

2. Дано: DABC - пирамида. DA ⊥ DB ⊥ DC; DA = DB = DC = a.

Найти: угол между прямой DA и плоскостью ABC.

Решение:

1. DO ⊥ пл. ABC.

2. φ = ∠DAO; Введем систему координат DABC; D(0; 0; 0); А(а; 0; 0); В(0; а; 0); С(0; 0; a) DO ⊥ (ABC). ΔABC - правильный.

(Ответ: .)

3. Дано: b; β; b ∩ β = M, b ⊥ β; b → b1, β → β1 (рис. 9).

Доказать, что b1 ⊥ β1.

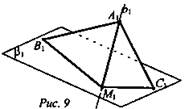
Результат движения:

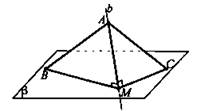
Решение: Выберем произвольные точки А ∈ β; В ∈ β; С ∈ β, b ⊥ β ⇒ AM ⊥ β и ΔАМВ и ΔАМС - прямоугольные. AM2 = АВ2 - ВМ2 = AС2 - СM2. При движении AB = A1B1; АМ = А1М1; АС = А1С1, А1М12 = A1B12 – B1M12 ⇒ A1M1 ⊥ B1M1. А1М12 = A1C12 – C1M12 ⇒ А1М1 ⊥ C1М1, таким образом, А1М1 ⊥ β1 (по признаку перпендикулярности прямой и плоскости, следовательно, b1 ⊥ β1, что и требовалось доказать.