Объем прямой призмы - Объем прямой призмы и цилиндра - ОБЪЕМЫ ТЕЛ

Цель урока:

- изучить с учащимися теорему об объеме прямой призмы;

- выработать навыки решения задач с использованием формулы объема прямой призмы.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний

1. Итоги самостоятельной работы, указать на типичные ошибки.

2. Ответить на вопросы, возникшие при выполнении домашней работы.

3. Повторение (фронтальный опрос).

а) Какой многогранник называется призмой?

б) Какая призма называется прямой?

в) Какая призма называется правильной?

г) Что является основанием правильной треугольной призмы?

д) Чем являются боковые грани призмы? Прямой призмы? Правильной призмы? (Параллелограммы, прямоугольники, равные прямоугольники.)

е) Сформулируйте свойства объемов?

ж) Сформулируйте следствие из теоремы об объеме прямоугольного параллелепипеда, в основании которого прямоугольный треугольник.

III. Изучение новой темы

Итак, мы с Вами повторили тот материал, который нам понадобится для изучения новой темы. Запишите в тетрадь тему сегодняшнего урока: «Объем прямой призмы».

Докажем теорему: Объем прямой призмы равен произведению площади основания на высоту.

Дано: прямая призма (рис. 1).

Доказать: V = S0 · h.

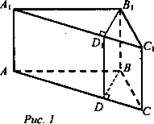
Доказательство:

1. АВСА1В1С1 - прямая призма. BD ⊥ AC (выберем высоту, которая делит ΔABC на два треугольника) проведем (BDD1) ⊥ (ABC), получим две призмы, основания которых прямоугольные треугольники, и они прямые.

V1 и V2 их объемы тогда

2. Рассмотрим n-угольную произвольную призму, ее можно разбить на (n-2) прямые треугольные призмы (рис. 2) с

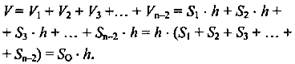
Итак

IV. Формирование умений и навыков учащихся

Решение задач по готовым чертежам, через кодоскоп на экран. Рассуждаем устно, делая промежуточные записи в тетради.

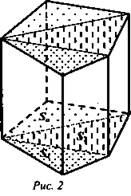
1. Дано: АВСА1В1С1 - прямая призма, АС = ВС, ∠ACB = 90°, BN = NA, ∠CNC1 = 45°, CC1 = 6 (рис. 3).

Найти: V.

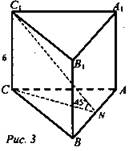
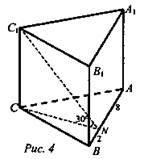
2. Дано: АВСА1В1С1 - прямая призма ∠ACB = 90°, ∠CNB = 90°, NB = 2, ∠AN = 8, ∠C1NC = 30° (рис. 4).

Найти: V.

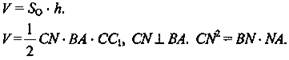
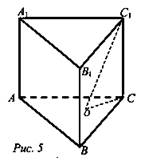
3. Дано: АВСА1В1С1 - прямая призма AB = 13; CB = 14; AC = 15 (рис. 5). О - центр описанной около ΔАВС окружности, ∠C1ОС = 30°.

Найти: V.

S - формула Герона

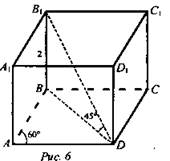
4. Дано: ABCDА1В1С1D1 - прямая призма, ABCD - ромб, ∠BAD = 60° (рис. 6). ВВ1 = 2, ∠B1DB = 45°.

Найти: V.

ΔABD - равносторонний.

5. Дано: АВСА1В1С1 - правильная призма. О - центр ΔАВС ∠C1OC = 30°, С1O = 4√3 (рис. 7).

Найти: V.

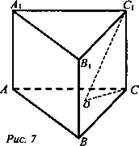
6. В тетрадь № 665.

Прочитали условия, ответили на мои вопросы:

1. Что представляет собой правильная шестиугольная призма?

2. Вы помните изображение ее на плоскости?

3. Какая диагональ в этой призме наибольшая?

4. Каким свойством обладает большая диагональ правильного шестиугольника? (Диаметр описанной окружности.)

5. Как связаны между собой сторона правильного шестиугольника и радиус описанной окружности? (Равны.)

А теперь самостоятельно оформите и решите задачу.

Дано: ABCDFM...M1 - правильная шестиугольная призма. AD1 = 8 см - наибольшая диагональ. ∠AD1D = 30° (рис. 8).

Найти: V.

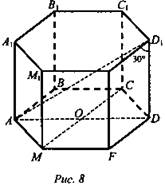
Решение: V= S0 · h. h = DD1 в ΔADD1, ∠D = 90°. ∠D1 = 30°, DD1 = AD1 · cos30°.

(Ответ: V= 72 cm3..

V. Подведение итогов

- Какие данные необходимы для определения объема прямой призмы?

Домашнее задание

П. 65 № 659 а), 663 а, б), 664.