Поурочные разработки по Геометрии 11 класс
Объем цилиндра - Объем прямой призмы и цилиндра - ОБЪЕМЫ ТЕЛ
Цели урока:
- изучить с учащимися теорему об объеме цилиндра;
- выработать навыки решения задач с использованием объема цилиндра.
Ход урока
I. Организационный момент
Собрать тетради с домашней работой для проверки.
1. Поверка домашней работы.
Задача № 659 а). Дано: АВСА1В1С1 - прямая призма. ∠BAC = 120°, АВ = 5 см, АС = 3 см, SBВ1С1C = 35 см2 (рис. 1).
Найдите: Vпр.
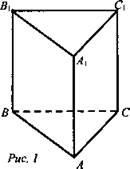
Решение: ![]()
1) ![]() .
.
2) Наибольшую площадь имеет боковая грань ВВ1С1С, так как сторона ВС - большая сторона ΔАВС (лежит против большего угла). Сторону ВС находим по теореме косинусов.
![]()
![]()
3) Найдем высоту призмы. ![]()
4) ![]()
(Ответ: ![]() )
)
Задача № 661. Дано: АВСА1В1С1 - прямая призма. АВ = ВС, ∠AВС = α; А1С = l, ∠АСА1 = β (рис. 2).
Найти: Vпр.
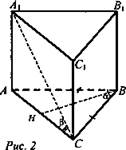
Решение:
1) ![]()
2) Из ΔАА1С: ![]()
3) Рассмотрим ΔABC. Проведем в нем высоту ВН; так как ΔАВС равнобедренный, то ВH является медианой и биссектрисой, т. е. ![]()
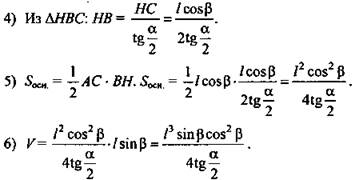
(Ответ: 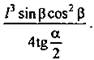 )
)
Задача № 663 в). Дано: правильная n-угольная призма. AB = a, AA1 = a, n = 6 (рис. 3).
Найти: Vпр.
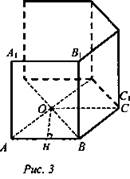
Решение:
1) ![]() .
.
2) Socн. = 6SΔAOB. h = а. ΔАОВ - правильный, ![]()
![]()
3) ![]()
(Ответ: 1,5а3√3.)
Задача № 663 г). Дано: правильная n-угольная призма. АВ = а, АА1 = а, n = 8.
Найти: Vпр.
Решение:
1) ![]()
2) Найдем Socн., Socн. = 8SΔAOB. Рассмотрим ΔАОВ - равнобедренный, ∠AOB = 360/8 = 45°. Проведем ОН ⊥ АВ; ОН - высота, медиана и биссектриса. ![]()
(Ответ: ![]() )
)
2. Доказать теорему об объеме пирамиды.
3. Решить задачу № 663 (г).
II. Актуализация опорных знаний
Что называется цилиндром, осью цилиндра, высотой цилиндра? Что является разверткой боковой поверхности цилиндра? Что является основанием цилиндра? Что является осевым сечением цилиндра? Площадь поверхности цилиндра? Дайте определение многоугольника вписанного в окружность и описанного около окружности.
III. Объяснение новой темы
1. Определение призмы, вписанной в цилиндр.
2. Определение призмы, описанной около цилиндра.
Теорема. Объем цилиндра равен произведению площади основания на высоту (рис. 4).
Дано: цилиндр радиуса r и высотой h.
Доказать: ![]()
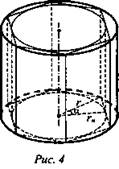
Доказательство: Введем следующие обозначения:
1) для цилиндра: Р - данный цилиндр, r - его радиус, S = πr2 - площадь основания, h - высота, V - объем.
2) для вписанной в цилиндр призмы: Fn - вписанная правильная n-угольная призма, Sn - площадь ее основания, h - высота (такая же, как у данного цилиндра).
3) для цилиндра, вписанного в призму Fn: Рn — вписанный цилиндр, rn - его радиус, h - высота (такая же, как у данного цилиндра Р и призмы Fn), Vn - объем. Впишем в данный цилиндр Р правильную n-угольную призму Fn, а в призму впишем цилиндр Pn. Объем призмы равен Sn · h, тогда Vn < Snh < V. Будем неограниченно увеличивать число n. Тогда rn → r при n → ∞. ![]() при n → ∞). Поэтому объем цилиндра Рn стремится к объему цилиндра Р.
при n → ∞). Поэтому объем цилиндра Рn стремится к объему цилиндра Р. ![]() Из неравенства следует, что
Из неравенства следует, что ![]() но
но ![]() Таким образом
Таким образом ![]()
IV. Формирование умений и навыков учащихся
I уровень
Решение задачи № 666 а), в).
а) Дано: цилиндр, r = 2√2 см, h = 3 см.
Найти: V.
Решение: ![]() (Ответ: 24π см3.)
(Ответ: 24π см3.)
в) Дано: цилиндр, r = h, V = 8π см3.
Найти: h.
Решение: ![]() так как r = h, то
так как r = h, то ![]()
![]() (Ответ: 2 см.)
(Ответ: 2 см.)
II уровень
- Какая из банок - широкая или узкая - вместительнее, если известно, что узкая втрое более высокая, но вдвое более узкая?
Дано: цилиндр Р1 и цилиндр Р2. R2 = 2r1 , h1 = 3h2.
Найти: V1 : V2.
Решение: ![]() (Ответ: объем второй банки больше в 4/3 раза объема первой банки..
(Ответ: объем второй банки больше в 4/3 раза объема первой банки..
Задача № 667.
Решение: ![]()
![]()
![]() (Ответ: ≈ 208 м.)
(Ответ: ≈ 208 м.)
Задача № 668.
Решение: Найдем объем цистерны. ![]()
![]()
![]() (Ответ: ≈ 1513 т.)
(Ответ: ≈ 1513 т.)
III уровень
Задача № 671 д) и задача по готовому чертежу или слайду (рис. 5).
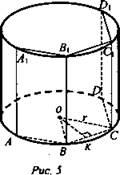
Решение:
1) ABCD...A1B1C1D1 - правильная n-угольная призма, вписанная в цилиндр; обозначим: СС1 = h, ОВ = r, Р — периметр, S - площадь основания призмы.
2) В ΔOКВ имеем: ![]()
![]() поэтому
поэтому ![]()
3) ![]()
4) 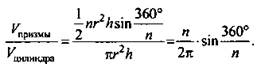 (Ответ:
(Ответ: ![]() )
)
Далее рассмотреть следующую задачу. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1, точка О - центр ее основания, BE1 = 8, ∠Е1ВЕ = 60°.
Найдите: а) объем призмы; б) объем описанного около призмы цилиндра; в) объем вписанного в призму цилиндра (рис. 6).
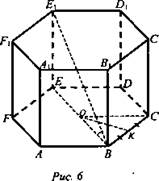
Решение: (слайд или готовый чертеж) а) ![]()
1) Из ΔВЕЕ1 найдем ЕЕ1. ![]()
![]()
2) Из ΔОВК: ![]()
![]()
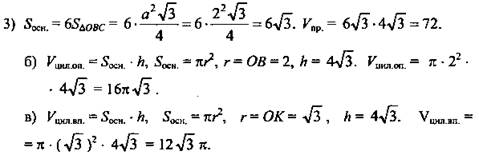
(Ответ: ![]() )
)
V. Подведение итогов
- Напишите формулу для определения объема цилиндра.
- Итак, мы доказали теорему об объеме цилиндра и еще раз убедились в практической необходимости умения вычислять объемы тел, зная их размеры.
Домашнее задание
П. 66, № 666 б), 669, 671 а), б).
Во сколько раз надо увеличить высоту цилиндра, если его радиус уменьшили в а раз, чтобы объем остался прежним.