Связь между координатами векторов и координат точек - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- ввести понятие радиус-вектора произвольной точки пространства;

- доказать, что координаты точки равны соответствующим координатам ее радиус-вектора, а координата любого вектора равна разности соответствующих координат его конца и начала;

- отработать понятие равных векторов при решении задач;

- отработать понятие коллинеарных и компланарных векторов при решении задач.

Ход урока

I. Проверка домашнего задания

Одного ученика из класса просим воспроизвести на доске решение № 415 а); д).

В это же время классу задаются вопросы:

1) Какие векторы называются коллинеарными?

2) Какие векторы называются компланарными?

Ответы иллюстрируем таблицей:

Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Компланарные векторы Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Задача № 415 а), д)

г) Дано:

Установить: компланарность данных векторов.

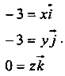
Решение: Если вектор можно разложить по векторам то векторы компланарны, - единичные векторы. х = -3; у = -3; z = 0. (Ответ: – компланарные векторы..

д) Дано: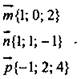

Установить: компланарность данных векторов.

Решение:

1. Векторы неколлинеарные, так как координаты этих векторов не пропорциональные друг другу числа.

2.

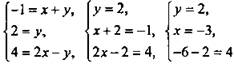(неверно, так как - 8 ≠ 4).

Ответ: - некомпланарные векторы.

II. Объяснение нового материала

1. Вектор, конец которого совпадает с данной точкой, а начало - с началом координат, называется радиус-вектором данной точки.

2. Координаты любой точки равны соответствующим координатам ее радиус-вектора.

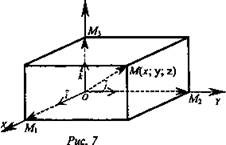
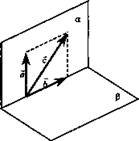
Пусть М (х; у; z) (рис. 7). Тогда М1 М2; М3 - точки пересечения с осями координат плоскостей, проходящих через точку М, перпендикулярно этим осям. Тогда по правилу параллелепипеда

Докажем, что

а) Если М1 лежит на положительной полуоси абсцисс, то х = ОМ1, а векторы

б) Если М1 лежит на отрицательной полуоси абсцисс, то а векторы

Поэтому

в) Если М1 совпадает с нулем, то

Аналогично

Подставим эти выражения в равенство (1), получим то есть

3. Выразим координаты вектора через координаты точек А(х1, у1; z1); В(х2, у2; z2) (рис. 8).

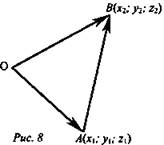
Значит,

Итак, каждая координата вектора равна разности соответствующих координат его конца и начала.

III. Закрепление знаний, умений и навыков учащихся

1. Задачи № 416; 417 записываются на доске и разбираются устно в классе, «комментированная работа с места». Предложенная запись заданий позволяет быстро отработать алгоритм решения.

Задача № 416 (устно)

Дано: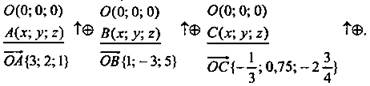

Задача № 417 (устно)

Дано: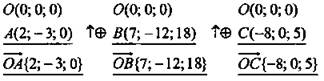

Найти:

2. Далее, работая над № 418 а), наполняем алгебраическим содержанием задания такого типа

Уровень А

Задача № 418 а)

Дано: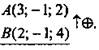

Найти:

Решение: (Ответ: .)

3. Переключаем внимание учащихся на заготовленный лист с тренировочными упражнениями по вариантам уровней Б и В. Проводим обучающую самостоятельную работу и коррекцию.

Уровень Б
I вариант	II вариант
1. Дано: Найти: х; у; z.	1. Дано: Найти: х; у; z.
Уровень В
2. Дано: Найти: х; у; z.	2. Дано: Найти: х; у; z.

Решение обучающей самостоятельной работы.

Вариант I

1. Дано: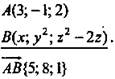

Найти: х; у; z.

Решение: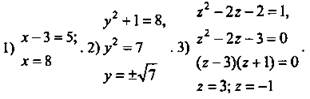

2. Дано: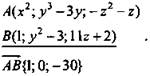

Найти: x; у; z.

Решение:

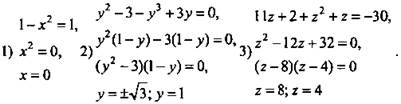
Вариант II

1. Дано: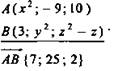

Найти: x; y; z.

Решение:

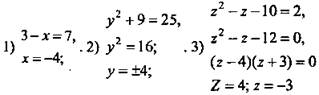
2. Дано: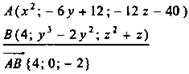

Найти: x; y; z.

Решение:

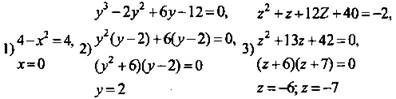
4. Далее решается Задача № 420. Учитель ведет запись на доске, ученик комментирует решение с места.

Задача № 420.

Задача предваряется вопросами:

- Какие векторы называются равными?

- Каково свойство равных векторов?

Ожидаемые ответы:

- Два вектора называются равными, если их длины равны и они с отправлены.

- Координаты равных векторов соответственно равны.

Дано: А(3; -1; 5), В(2; 3; -4), С(7; 0; -1), D(8; -4; 8).

Доказать:

Решение: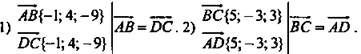

5. Задача № 422 а) подводит итог урока, запись решения проводит вызванный к доске ученик.

Задача № 422 а). Дано: А(-2; -13; 3), В(1; 4: 1), С(-1; -1; -4), D(0; 0; 0).

Установить: А; В; С; D; лежат ли в одной плоскости.

Решение:

Так как, сравнивая координаты векторов, мы видим, что они - непропорциональные числа, то делаем вывод, что векторы - неколлинеарные.

2) Проверим компланарность векторов.

Предположим, что вектор можно разложить по векторам и

Если коэффициенты разложения х; у находятся однозначно, то векторы компланарны и данные точки лежат в одной плоскости.

Составим и решим систему уравнений.

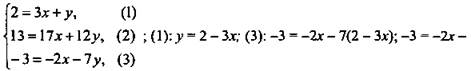
Проверим справедливость (2) при найденных значениях х и у.

(верно).

Вывод: векторы - компланарны.

(Ответ: точки А; В; С; D лежат в одной плоскости.)

IV. Подведение итогов

- Итак, в ходе урока мы изучили понятие радиус-вектора точки, правило нахождения координат вектора, понятие равных векторов. Повторили понятия коллинеарных и компланарных векторов.

Домашнее задание

Уровень А: № 418 б), в).

Уровень Б: ⊕ № 419; 412 а), б).

Уровень В: ⊕ № 422 (б); п. 24 (10 кл.) № 366, разобрать решение.