Зачет по теме: «Тела вращения» - урок 4 - КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Проведение зачета по карточкам

I уровень

Карточка № 1

1. Объясните, какое тело называется цилиндром.

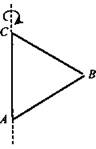
2. Какая фигура образуется при вращении ΔAВС вокруг оси (достроить). Вычислите полную поверхность тела вращения, которое получается в результате вращения ΔABC вокруг его стороны АС, если АС = 8 см, ВС = 5 см.

3. Высота конуса равна 6 см, а образующая наклонена к плоскости основания под углом в 30°. Найдите площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60.

4. Радиус шара равен R. Найдите площадь поверхности вписанного в шар куба.

Карточка № 2

1. Объясните, какое тело называется конусом.

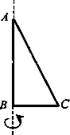
2. Вычислите полную поверхность тела вращения, которое получается в результате вращения ΔАВС вокруг его стороны АВ, если АВ = 4 см, ВС = 3 см.

3. Радиус шара равен 8 см. Через конец радиуса, лежащего на сфере, проведена плоскость под углом 45° к радиусу. Найдите площадь сечения шара этой плоскостью.

4. Куб с ребром а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Карточка № 3

1. Объясните, какое тело называется усеченным конусом.

2. Вычислите площадь полной поверхности тела вращения, если AD = 8 см, ВС = 6 см.

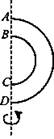
3. Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 90°. Найдите площадь сечения, если высота цилиндра равна 6 см, а расстояние между осью цилиндра и секущей плоскостью равно 3 см.

4. Около шара радиуса R описан правильный конус. Найдите площадь поверхности конуса.

Карточка № 4

1. Объясните, какая поверхность называется сферой и какое тело называется шаром.

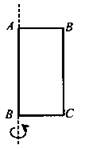
2. Вычислите полную поверхность тела вращения, которое получается в результате вращения прямоугольника вокруг его стороны AD, если АВ = 3 см, АС = 5 см.

3. Осевое сечение цилиндра - квадрат, диагональ которого равна 12 см. Найдите площадь боковой поверхности цилиндра.

4. В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60°. Найдите площадь сферы.

II уровень

Карточка № 1

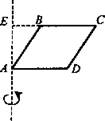
1. Выведите формулу площади полной поверхности цилиндра. ABCD - ромб, АВ = a, BE = b. Найдите полную поверхность тела вращения.

2. На поверхности шара выбраны точки А и В так, что АВ = 40 см, а расстояние от центра шара до прямой АВ равно 15 см. Найдите площадь сечения шара, проведенного через точки А и В на расстоянии 7 см от центра шара.

3. Плоскость, параллельная оси цилиндра, пересекает основание цилиндра по хорде, которая видна из центра этого основания под углом а. Диагональ образовавшегося сечения наклонена к плоскости основания под углом р. Радиус цилиндра равен R. Найдите: а) площадь данного сечеиия; б) площадь осевого сечения.

Карточка № 2

1. Выведите формулу площади полной поверхности конуса.

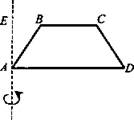
2. ABCD - равнобокая трапеция, AD = a, ВС = b, CD = с. Найдите полную поверхность тела вращения.

3. На поверхности шара выбраны точки А и В так, что АВ = 40 см, а расстояние от центра шара до прямой АВ равно 15 см. Через точки А и В проведено сечение, площадь которого равна 576π см2. Найдите расстояние от центра шара до плоскости сечения.

4. Плоскость, параллельная оси цилиндра, пересекает основание цилиндра по хорде, составляющей с диагональю данного сечения угол р. Радиус основания цилиндра, проведенный в один из концов хорды, образует с плоскостью сечения угол а. Высота цилиндра равна Н. Найдите: а) площадь данного сечения; б) площадь осевого сечения.

Карточка № 3

1. Выведите формулу уравнения сферы.

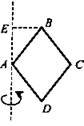
2. ABCD - ромб, АС = а, ВС = с, ВЕ = b. Найдите полную поверхность тела вращения.

3. Высота конуса равна Н и составляет с образующей конуса угол α. Найдите: а) площадь сечения, проведенного через середину высоты конуса параллельно плоскости основания; в) площадь сечения, проведенного через две образующие, угол между которыми равен р.

4. Плоскость, параллельная оси цилиндра, пересекает его основание по хорде, стягивающей угол α. Площадь осевого сечения цилиндра равна S. Найдите площадь образовавшегося сечения.

Карточка № 4

1. Выведите формулу площади полной поверхности усеченного конуса.

2. ΔАВС - равнобедренный, АС = а, ВС = с, BE = b. Найдите полную поверхность тела вращения.

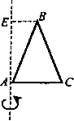
3. Хорда основания конуса равна а и видна из центра основания под углом α. Найдите: а) площадь сечения, проведенного через середину высоты конуса параллельно плоскости основания; в) площадь сечения, проведенного через данную хорду и вершину конуса, если образующая, проходящая через конец хорды, составляет с хордой угол β.

4. Сечение цилиндра, параллельное оси, имеет площадь Q и пересекает основание цилиндра по хорде, стягивающей дугу α. Найдите площадь осевого сечения цилиндра.