Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами - ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются дифференциальные уравнения вида

y’’ + py’ + qy = 0,

где р и q — заданные постоянные.

Для нахождения общего решения данного дифференциального уравнения строится соответствующее ему характеристическое уравнение, имеющее вид

k2 + pk + q = 0,

и определяются его корни.

При этом возможны следующие ситуации, зависящие от знака дискриминанта D характеристического уравнения.

1. D = р2 - 4q > 0

В этом случае характеристическое уравнение имеет два разных корня

,

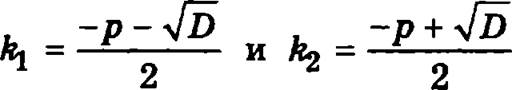а общее решение уравнения имеет вид

где С1 и С2 — произвольные постоянные.

2. D = р2 – 4q = 0

В этом случае характеристическое уравнение имеет два одинаковых корня

а общее решение уравнения

С1 и С2 — произвольные постоянные.

3. D = р2 – 4q < 0

В этом случае характеристическое уравнение имеет два комплексно-сопряженных корня

а общее решение исходного однородного линейного дифференциального уравнения представляется в виде

Пример. Найти общее решение дифференциального уравнения у’’ + 27у’ + 140у = 0.

Строим соответствующее данному дифференциальному уравнению характеристическое уравнение, учитывая, что в рассматриваемом случае р = 27, a q = 140:

k2 + 27k + 140 = 0.

Дискриминант характеристического уравнения равен

D = 272 - 4 ∙ 140 = 729 - 560 = 169 > 0.

Следовательно, уравнение имеет два разных корня:

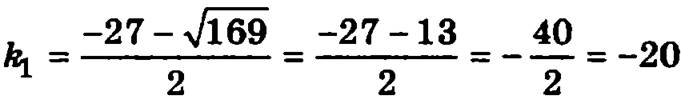
и

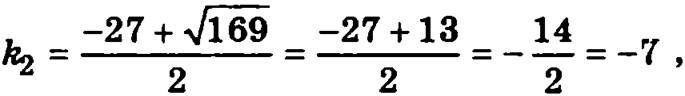
а общее решение исходного однородного линейного дифференциального уравнения имеет вид