Путешествие в историю математики - Свечников А. А. 1995
Числа количественные и порядковые. Четные и нечетные
Натуральный ряд чисел позволяет ответить на вопрос, сколько предметов в том или другом множестве. Кроме того, он позволяет расположить предметы в определенной последовательности и выяснить, которым по порядку идет тот или иной предмет — шестым, седьмым или четырнадцатым и т. п. В первом случае числа называют количественными (два, четыре, семь), а во втором — порядковыми (седьмой, десятый и т. д.).
Порядковые числа натурального ряда позволяют, скажем, в шеренге солдат быстро определить место каждого человека, стоит лишь выполнить команду: «По порядку номеров рассчитайся!»
Деление чисел на количественные и порядковые было известно с самых древних времен.
Все числа натурального ряда можно распределить на два бесконечных ряда — числа нечетные и числа четные. Вот начала этих рядов.
Числа нечетные: 1, 3, 5, 7, 9, 11, 13,15, 17, 19, 21, 23...
Числа четные: 2, 4, 6, 8,10, 12, 14, 16, 18, 20, 22...
В натуральном ряду числа нечетные и четные строго чередуются. За нечетным числом обязательно следует четное, за ним — нечетное.
Четные и нечетные числа были известны еще египтянам, хотя они их так и не называли. В Греции подобное распределение чисел приписывают Пифагору (VI в. до н. э.) и его последователям. Позже понятие о четных и нечетных числах получило довольно широкое распространение, что подтверждается игрой «в чет и нечет», вошедшей тогда в моду среди привилегированных слоев греков. Деление чисел на четные и нечетные вызывало интерес к свойствам натурального ряда чисел у многих математиков Греции.
Ряд нечетных чисел обладает интересными свойствами. Убедитесь в этом сами:

Из приведенной таблицы видно, что сумма двух первых рядом стоящих нечетных чисел дает произведение 2 • 2. Сумма трех нечетных стоящих рядом чисел дает произведение 3 • 3. Сумма первых восьми рядом стоящих нечетных чисел даст 8•8. Сумма тринадцати рядом стоящих нечетных чисел, по-видимому, даст 13 • 13 = 169. Проверьте это утверждение.
Сделанное наблюдение можно строго доказать.
Натуральный ряд чисел можно разделить на три группы. Первая — это единица; вторая группа — это числа простые, т. е. такие, которые делятся на единицу и на самих себя и больше никаких делителей не имеют, например: 2, 7, 19 и др. Третья группа — числа составные, т. е. составленные из множителей, представляющих собой простые числа. К ним относятся, например, числа 4, 6, 8, 9, 15, 20 и др. Каждое из составных чисел можно выразить произведением нескольких простых чисел. Например: 20 = 2 • 2 • 5; 18 = 2 • 3 • 3; 34 = 2 • 17 и т. д.
Понятия о простых числах и составных сложились также у пифагорийцев. Название этим группам чисел было присвоено позже. В книге Евклида «Начала» речь идет как о числах простых, так и о составных. К простым числам ученый отнес и единицу. Исключение единицы из группы простых чисел произошло значительно позже. Это сделал великий математик Леонард Эйлер (1707 — 1783). Эйлер родился и получил образование в Швейцарии, а в 1727 г. был приглашен в Петербургскую академию наук. Он указал, что единица, будучи началом всех целых чисел, не является ни простым, ни составным числом, так как у единицы только один делитель, равный числу один. О числе два, которое теперь с полным основанием отнесено к простым числам, у древних греков существовали разные мнения. Одни из них считали это число простым, другие не относили его к таковым.
Геометрические фигуры пифагорийцев.
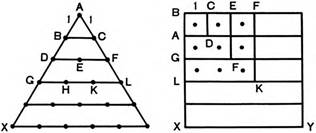
Пифагорийцы тесно связывали числа с геометрическими фигурами. Они составляли из камешков или ракушек разнообразные фигуры, которые содержали определенное число предметов, а также изображали числа точками, расположенными в определенном порядке в геометрических фигурах. Таким образом числа получались треугольные, квадратные и др.