Основное свойство дроби - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ - ОБЫКНОВЕННЫЕ ДРОБИ

Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей.

Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. При этом рекомендуется излагать материал без опоры на понятия НОД и НОК. Умение приводить дроби к общему знаменателю используется для сравнения дробей.

При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа. Что касается сложения и вычитания смешанных чисел, которые не находят активного применения в последующем изучении курса, то учащиеся должны лишь получить представление о принципиальной возможности выполнения таких действий.

Информация для учителя

Основное свойство дроби используется:

1) при сокращении дробей, то есть когда данную дробь заменяют равной ей дробью с меньшим числителем и знаменателем;

2) при приведении дробей к новому знаменателю, то есть когда данную дробь заменяют равной ей дробью, знаменатель которой делится на знаменатель данной дроби.

ОСНОВНОЕ СВОЙСТВО ДРОБИ (2 ч)

Урок 21. Основное свойство дроби

Цели: ввести понятие основного свойства дроби; учить применять основное свойство дроби; формировать навык нахождения наибольшего общего делителя и наименьшего общего кратного чисел; воспитывать аккуратность.

Ход урока

I. Организационный момент

II. Анализ контрольной работы

1. Ознакомить учащихся с результатами контрольной работы.

2. Решить задания, в которых допущено наибольшее количество ошибок.

III. Устный счет

1. Прочитайте числа: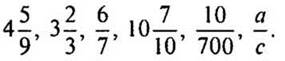

(Дробь, числитель которой а, а знаменатель с.)

— Назовите числитель и знаменатель каждой дроби.

— Что показывает знаменатель дроби? (На сколько равных частей разделили целое.)

— Что показывает числитель дроби? (Сколько таких равных частей взяли.)

2. Переведите дроби в неправильную дробь: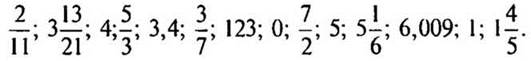

— На какие группы можно разделить данные числа? (Дробные — обыкновенные и десятичные дроби; натуральные; число нуль.)

3. Расскажите, как получаются дроби: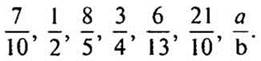

(Целое разделили на 10 равных частей и взяли 7 таких частей; целое раздели на b равных частей и взяли а таких частей.)

— Какие значения могут принимать а и b? (а — любое натуральное число или нуль, b — любое натуральное число.)

IV. Сообщение темы урока

— Сегодня мы познакомимся с основным свойством дроби и научимся его применять. А знаете, в каком веке в русском языке появилось слово «дробь»? (В VIII веке.)

V. Изучение нового материала

1. Подготовительная работа (устно).

— Найдите наибольший общий делитель числителя и знаменателя дробей: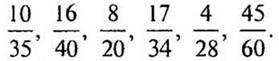

— Давайте вспомним, когда и как возникают дроби. У людей с древних времен появилась необходимость измерять время, расстояния, площади, углы и другие величины. Потребность в более точном измерении привела к тому, что используемые единицы измерения стали делить на части. А это привело к появлению дробей.

Дроби образуются:

1) в результате деления предмета (единицы или целого) на равные части;

2) при измерении величин, когда единица измерения не укладывается целое число раз в измеряемом объекте;

3) при делении натуральных чисел.

2. Работа над новой темой.

— Прочитайте в учебнике на стр. 34 § 8.

— На сколько равных частей разделили круг сначала? (На 4 части.)

— Сколько частей закрасили? (3 части.)

— На сколько равных частей потом разделили четвертую часть круга? (На 5 частей.)

— На сколько частей оказался разделенным весь круг? (На 20 частей.)

— Сколько частей в трех закрашенных четвертях круга? (9 частей.)

— Прочитайте основное свойство дроби.

— Запишем в тетрадь:

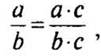где с — натуральное число;

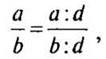где d — натуральное число и d — общий делитель а и b.

Определение. Равные дроби — различные обозначения одного и того же числа: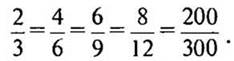

— Приведите примеры равных дробей. (Записать на доске.)

3. Работа с учебником.

— Прочитайте текст в учебнике на стр. 35 под рубрикой «Говори правильно».

— Прочитайте равенство двух дробей, записанных на доске, разными способами.

VI. Физкультминутка

VII. Работа над задачей

1. № 233 (1) стр. 37 (у доски и в тетрадях).

— Прочитайте задачу. Зная расстояние и скорость, что можно найти? (Время.)

— Зная весь путь и расстояние, которое прошли до привала, что можно найти? (Путь, который пройдут школьники после привала.)

— Зная расстояние, которое проедут школьники со скоростью 15,3 км/ч, что можно найти? (Время на путь после привала.)

— Как найти, сколько времени школьники были в походе? (Сложить время до привала, время после привала и время, затраченное на привал.)

Решение:

1) 48,6 : 12,15 = 4 (ч) — было в пути до привала.

2) 79,2 — 48,6 = 30,6 (км) — проехали после привала.

3) 30,6 : 15,3 = 2 (ч) — были в пути после привала.

4) 4 + 2,5 + 2 = 8,5 (ч) — были в походе.

(Ответ: 8,5 ч.)

2. Решите устно задачу.

Торт разрезали на 8 равных частей. Одну из них разрезали еще на 2 равные части. Какую часть пирога составляет одна маленькая часть? (1/16.)

VIII. Закрепление изученного материала

1. № 211 стр. 35 (устно).

Можно разобрать решение по вопросам вместе с учителем, а можно дать возможность учащимся самостоятельно объяснить, почему дроби равные.

Разбор по вопросам учителя:

— Что обозначает дробь 3/5? (Целое или круг разделили на 5 равных частей и взяли 3 такие части.)

— На сколько равных частей мы потом разделили пятую часть круга? (На 3 части.)

— На сколько частей оказался разделенным весь круг? (На 15 частей.)

— Сколько частей в 3 взятых пятых круга? (9 частей.)

Развернутый ответ учащихся:

Мы круг раздел или на 5 равных частей и закрасили 3 такие части, затем каждую пятую часть круга мы разделили еще на 3 равные части. Тогда весь круг оказался разделенным на 5 · 3 = 15 частей, а в трех пятых круга будет 3 · 3 = 9 таких частей, поэтому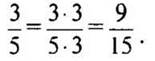

2. Практическая работа.

№ 215 стр. 36 (на доске и в тетрадях).

— Что такое координатный луч?

— Какой вывод можно сделать? (Равные дроби на координатном луче изображаются одной и той же точкой.)

— Прочитайте равенство дробей разными способами.

— Назовите наименьшее и наибольшее из чисел.

3. № 216 стр. 36 (самостоятельно с последующей проверкой, в это время один ученик работает на обратной стороне доски).

— Что можете сказать об этих дробях? (Они равные.)

— Почему? (Мы использовали основное свойство дроби.)

— Как из данных дробей получить равные им дроби? (Умножить или разделить числитель и знаменатель на одно и то же натуральное число.)

— Чем мы воспользовались? (Основным свойством дроби.)

IX. Самостоятельная работа (с последующей проверкой)

а) № 214 стр. 36 (ученики работают цветными карандашами).

Проверка:

— Что обозначают дроби 3/4 и 6/8? (Целое или отрезок разделили на 4 равные части и взяли 3 такие части и второй отрезок такой же длины разделили на 8 равных частей и взяли 6 таких частей.)

— Что можете сказать о цветных частях данных отрезков? (Равны.)

— Что можете сказать о данных дробях? (Дроби равны.)

— Какой вывод можно сделать? (Равные дроби изображаются равными отрезками.)

б) № 217 стр. 36.

— Что применяли при решении? (Основное свойство дроби.)

X. Закрепление изученного материала

1. Не выполняя вычислений, объясните, почему возведение в квадрат выполнено неверно:

а) 732 = 499; б) 262 = 9006; в) 542 = 2508; г) 1052 = 1025.

Решение:

Выполним прикидку:

а) 702 = 4900 , 499 < 4900;

б) 302 = 900, 900 < 9006;

в) 42 = 16, а в числе 2508 последняя цифра 8;

г) 1002 = 10 000, 1025 < 10 000.

2. № 230 (а) стр. 37 (самостоятельно с последующей самопроверкой).

Лучше записывать в виде произведения степеней.

— Что значит разложить число на простые множители?

Решение:

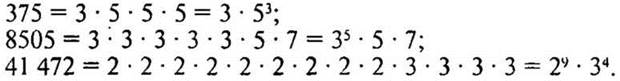
3. Устно найдите наибольший общий делитель и наименьшее общее кратное чисел: 50 и 60; 15 и 45; 3 и 15; 5 и 11; 6 и 8; 15 и 12.

XI. Подведение итогов урока

— Сформулируйте основное свойство дроби.

— Чем являются равные дроби? (Различными записями одного и того же числа).

Домашнее задание

Учебник, стр. 35 (прочитать текст под рубрикой «Говори правильно»), № 207 стр. 33, № 221 (а, б) стр. 36, № 239 (а), 240 (а, в), 241 (а) стр. 38.

Дополнительный материал

Шутка

Я докажу, что в течение целого года вам почти некогда учиться в школе. В году 365 дней. Из них 52 воскресенья, 10 других дней отдыха. Отпадает 62 дня. Летние и зимние каникулы - не меньше 100. Минус еще 100 дней. Ночью в школу не ходят, а ночи составляют половину года, следовательно, еще 183 дня минус. Остается 20 дней, но ведь не весь день продолжаются занятия, а не более четверти дня. Остается всего 5 дней. Многому ли тут можно научиться?